小波最近邻抽样回归耦合模型原理及其应用

7.5.1.1　基本思路

采用快速小波变换算法对水文时间序列进行小波分解，得到小波变换序列，然后根据最近邻（相似性）原理分别建立各小波变换序列的最近邻抽样回归模型（nearest neighbor bootstrap regressive model，简称NNBR模型），最后将得到的各小波变换序列的预测值按照小波逆变换算法进行重构即可得到原始水文时间序列的预测值（王文圣等，2005），称为小波最近邻抽样回归耦合模型（简称W-NNBR耦合模型）。

7.5.1.2　最近邻抽样回归模型

根据研究对象的不同，NNBR模型可以分为单因子NNBR模型和多因子NNBR模型两种形式。本节研究的逐月地下水埋深序列采用单因子NNBR模型。

1.单因子NNBR模型构造

已知单变量小波变换序列Xt（t=1，2，…，n），Xt依赖前P个相邻历史值Xt-1，Xt-2，…，Xt-P。定义Dt=（Xt-1，Xt-2，…，Xt-P），称Dt为特征矢量，Xt为Dt的后续值（t=P+1，P+2，…，n）。已知当前特征矢量Di=（Xi-1，Xi-2，…，Xi-P），如何预测其后续值Xi呢？最近邻预测的基本思想是（王文圣等，2001；王文圣等，2005）：在已有的特征矢量Dt（t=P+1，P+2，…，n）中，总有K个与当前特征矢量Di最近邻，从而在Dt中可得到K个最近邻特征矢量，记为D1（i），D2（i），…，DK（i），其对应的后续值分别为X1（i），X2（i），…，XK（i）。最近邻是根据Di与Dt间的欧氏距离来判断，距离越小，Di与Dt越近邻，欧氏距离计算见式（7.27）。K个最近邻特征矢量D1（i），D2（i），…，DK（i）与Di间的欧氏距离记为d1（i），d2（i），…，dK（i）。若dj（i）越小，说明Dj（i）与Di越近邻，则Xi=Xj（i）的可能性Wj（i）越大（j=1，2，…，K），即Xj（i）对Xi的贡献越大。将wj（i）记为Xj（i）的抽样权重，可见wj（i）与欧氏距离dj（i）成反比。

式中　dj（i）——Di与Dt间的欧氏距离；

Dij、Dtj——Di、Dt的第j个元素；

P——特征矢量维数。(www.xing528.com)

根据上述思想，单因子NNBR模型的基本形式为：

式中——Xi的预测值；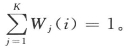

2.K、P和wj（i）的确定

一般最近邻数K=int（），int表示取整；m为特征矢量个数，当研究对象为单变量时，m=n-P。对于单变量时间序列，特征矢量维数P为与Xt相关的前相邻历史值个数，由时间序列自相关图和偏相关图确定，同时要求满足P≥2（王文圣等，2005）。抽样权重，其中，j=1，2，…，K，当K确定后，wj（i）只需计算一次。

5.1.1.3　W-NNBR耦合预测模型

采用A Trous重构算法将各小波变换序列NNBR模型预测值进行叠加，得到原始水文时间序列W-NNBR耦合模型预测值。重构过程为：

式中　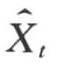——Xt的预测值；

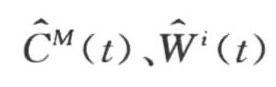——CM（t）、Wi（t）的预测值。