小波随机耦合模型在地下水动态变化预测中的应用

现以三江平原八五三农场为例，根据八五三农场1991～2004年的逐月地下水埋深实测序列资料建立小波随机耦合模型，将2005年的逐月地下水埋深实测序列资料作为预留检验，对当地地下水埋深动态进行预测。

1.实测逐月地下水埋深序列平稳化处理

由图7.1可以看出，八五三农场实测逐月地下水埋深序列Ht为一非平稳时间序列，同时Ht具有非常明显的以年（12个月）为周期的变化规律，因此可以对序列Ht进行季节差分。由于Ht在均值水平上不平稳，因此认为只需对其进行一次差分即可达到平稳，即：

式中　B——后移算子。

通过差分，使得逐月地下水埋深序列Ht由非平稳序列转化为平稳序列Xt，如图7.17所示。

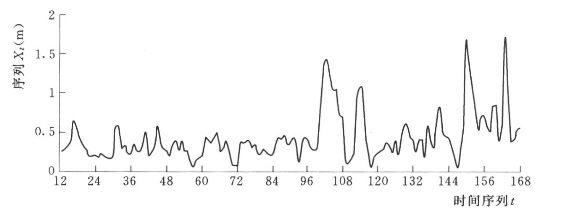
图7.17　八五三农场逐月地下水埋深差分序列变化曲线

2.逐月地下水埋深差分序列小波分解与重构

采用前述的A Trous算法，取尺度数P=2，对八五三农场1991～2004年的逐月地下水埋深差分序列Xt进行分解。由于需要用到边界以外的数据，因此需要进行边界延拓。传统的小波变换边界延拓方法有零值延拓、边界重复延拓、对称延拓、线性延拓、抛物线延拓、平滑延拓、多点拟合延拓、AR模型预测延拓（张郁山等，2003；王文圣等，2005；袁礼海等，2006；于枝伶，2007）等。信号不同，延拓方法也会不同。经过分析，如果采用边界重复延拓，则在边界以外无法保持序列原有趋势，而如果采用线性延拓，则会夸大序列原有趋势。因此，采用上述两种方法均会产生边界以外数据失真的问题。为很好解决边界延拓问题，本节采用边界重复延拓和线性延拓相结合（各占50%权重）的方法，得到小波分解序列｛W1（t），W2（t），C2（t）｝，见图7.18（a）、（b）、（c）。将各小波分解序列进行叠加，得到重构序列，如图7.18（d）所示。由图7.18（d）可以看出，重构过程与图7.17中序列Xt变化过程完全一致，因此，采用A Trous算法对八五三农场逐月地下水埋深差分序列进行分解是可行的。

3.小波变换序列成分识别

采用公式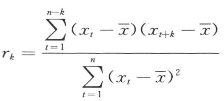和计算各小波变换序列的自相关系数和方差谱密度，并绘制自相关图和方差谱密度图，见图7.19和图7.20。根据图7.18、图7.19和图7.20分析各小波变换序列的变化特性，可以近似认为W1（t）代表序列Xt的随机项，W2（t）代表序列Xt的周期项，C2（t）代表序列Xt的趋势项。

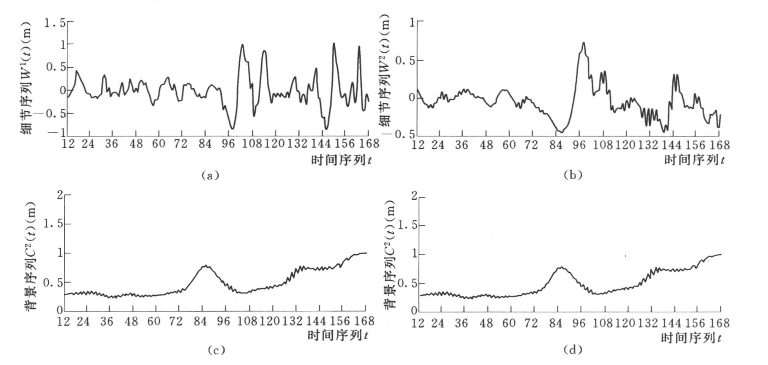
图7.18　八五三农场逐月地下水埋深差分序列小波分解与重构

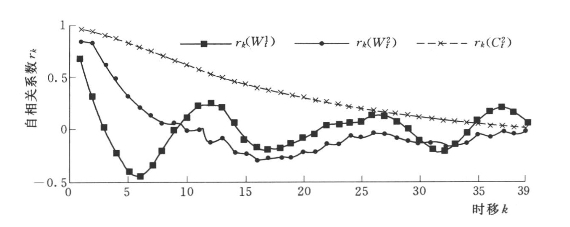
图7.19　各小波变换序列自相关图

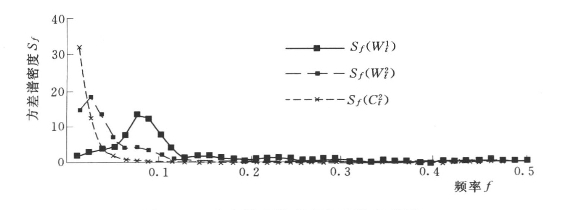
图7.20　各小波变换序列方差谱密度图

4.小波变换序列互相关分析

采用公式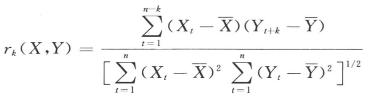分别计算各小波变换序列的互相关系数，绘制互相关图，并加绘95%容许限，如图7.21所示。

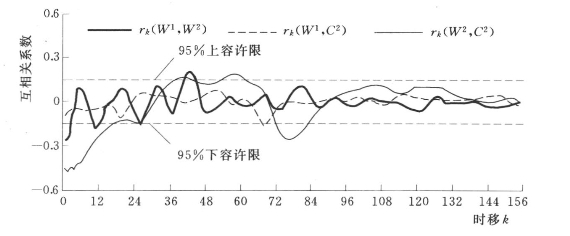
图7.21　各小波变换序列互相关图

由图7.21可以看出，各小波变换序列互相关系数基本上落在95%容许限范围以内，且趋近于0。因此，各小波变换序列互相关性较小，可以认为小波变换序列W1（t）、W2（t）和C2（t）两两独立。上述互相关分析结果表明，小波变换序列W1（t）、W2（t）和C2（t）成分单一，比序列Xt要简单，因此分析和处理Xt就转嫁为对W1（t）、W2（t）和C2（t）进行处理。

5.建立细节序列W1（t）的随机模型

通过计算机编程计算，小波分解细节序列W1（t）的均值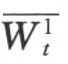=-0.0160≈0，方差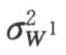=0.1131，偏态系数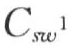=0.1053，趋近于0，所以认为序列W1（t）近似于正态分布，不必进行正态性转化。

对序列W1（t）分别进行自相关分析和偏相关分析，自相关图具有拖尾性，而偏相关图具有截尾性，所以初步判定模型形式为AR（p）模型。参考相关文献，判定模型阶数为1，属于AR（1）模型（丁晶等，1997；付强，2005）。对AR（1）模型参数进行计算，建立如下自回归模型：

采用BIC准则对AR（p）模型的阶数进行进一步识别。当p=1时，BIC达到最小值，BIC（1）=156ln0.0505+ln156=-460.7321。这说明初步确定的模型阶数为1阶是合适的。(www.xing528.com)

采用自相关系数综合检验法检验残差项εt是否为独立序列。经过计算，统计量Q=42.2592，n=156，取m=n/4=156/4=39，查χ2表得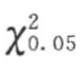=53.3840，Q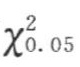＜，所以εt为独立随机序列。对独立随机序列εt的正态性进行检验：均值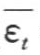=-0.0013≈0，方差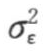=0.0627，偏态系数Cs（e）=0.1152，趋近于0，因此近似认为εt～（0，0.0627）正态分布。因此，细节序列W1（t）随机项模型为：

6.建立细节序列W2（t）和背景序列C2（t）的自回归模型

细节序列W2（t）和背景序列C2（t）为确定成分，可以借助于水文学中的自回归模型（略去随机变量εt）对序列W2（t）和C2（t）进行描述。

分别对序列W2（t）和C2（t）进行自相关分析和偏相关分析，并采用BIC准测，判定所需建立的W2（t）和C2（t）自回归模型阶数分别为4阶和5阶。

对于序列W2（t），选定k=1，2，3，4（偏相关系数超出95%容许限范围），则略去随机变量εt的AR（4）模型为：

对于序列C2（t），选定k=1，2，3，4，5（偏相关系数超出95%容许限范围），则略去随机变量εt的AR（5）模型为：

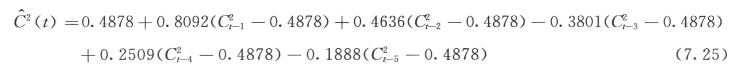
7.模型组合

将上述各小波变换序列模型进行叠加并还原，就可以得到八五三农场逐月地下水埋深小波随机耦合模型，即：

8.小波随机耦合模型拟合

采用建立的逐月地下水埋深小波随机耦合模型对八五三农场1991～2004年的逐月地下水埋深进行拟合，如图7.22所示。从图7.22中可以看出八五三农场逐月地下水埋深小波随机耦合模型拟合效果良好。

9.小波随机耦合模型精度检验

采用所建小波随机耦合模型的拟合数据进行拟合效果检验，并采用未参加建模的2005年逐月地下水埋深实测数据进行试报效果检验，具体计算结果见表7.7。

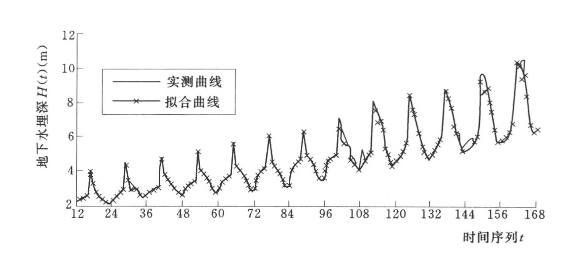
图7.22　八五三农场逐月地下水埋深小波随机耦合模型拟合曲线

表7.7　小波随机耦合模型精度检验结果

根据有关文献可知，C、p、E2和E3均达到1级标准，E1达到2级标准（陈南祥，1999）。因此，所建八五三农场地下水埋深小波随机耦合模型拟合效果良好，预测精度较高，可用于预测八五三农场未来地下水埋深。

10.地下水埋深预测

现采用所建小波随机耦合模型预测八五三农场2006～2009年逐月地下水埋深，地下水埋深预测值及预测曲线分别见表7.8和图7.23。从表7.8和图7.23中可以看出，如果仍然采用过去的地下水开采模式，八五三农场的地下水位将会持续下降。2006～2009年地下水埋深年降幅分别为0.62m、0.45m、0.56m和0.37m，未来4年地下水埋深平均年降幅为0.5m左右。因此，八五三农场应加大地下水管理力度，以保护当地有限的地下水资源。

表7.8　八五三农场逐月地下水埋深小波随机耦合模型预测值（2006～2009）　单位：m

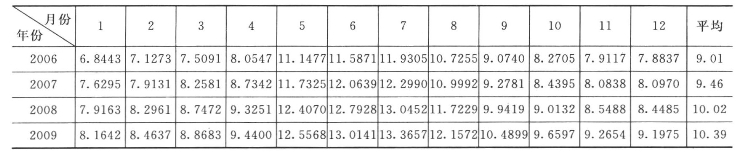
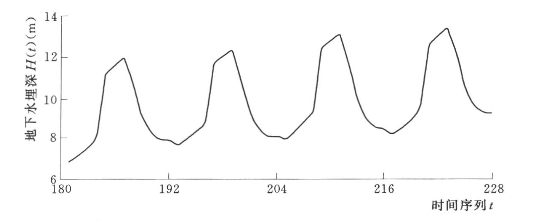
图7.23　八五三农场逐月地下水埋深小波随机耦合模型预测曲线（2006～2009）