小波神经网络模型在八五三农场地下水动态变化预测中的成功应用

现以三江平原八五三农场为例，采用MATLAB7.0编程处理数据。根据八五三农场1991～2004年的逐月地下水埋深实测序列资料建立WANN模型，将2005年的逐月地下水埋深实测序列资料作为预留检验，对当地地下水埋深动态进行模拟和预测。

1.实测序列的小波分解与重构

采用前述的A Trous算法，取尺度数P=2，对八五三农场1991～2004年的逐月地下水埋深实测序列H（t）进行分解，分解过程中采用线性边界延拓方法（袁礼海等，2006），得到小波分解序列｛W1（t），W2（t），C2（t）｝，如图7.14所示。图7.14（a）中，C0（t）=H（t），代表原始序列；图7.14（b）中，W1（t）代表原序列的随机项，W2（t）代表原序列的周期项；图7.14（c）中，C2（t）代表原序列的趋势项。将各小波分解序列进行叠加，得到重构序列，如图7.14（d）所示。由图7.14可以看出，重构过程与实测过程完全一致，因此，采用A Trous算法对八五三农场逐月地下水埋深实测序列进行分解是可行的。

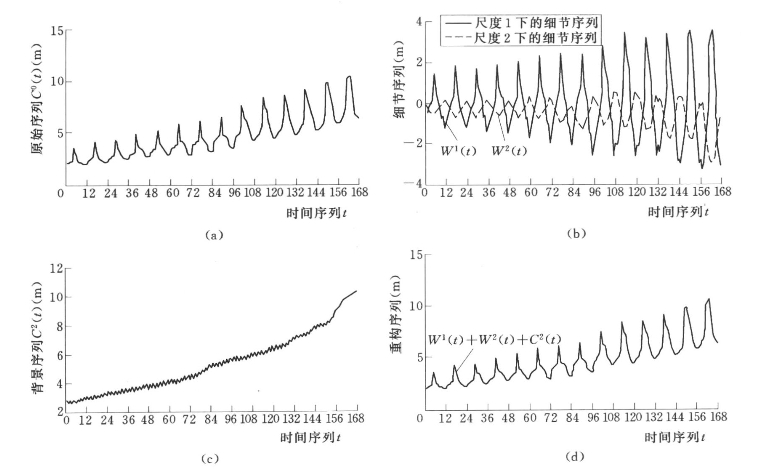
图7.14　八五三农场逐月地下水埋深实测序列小波分解与重构（1991～2004）

2.输入、输出样本对的确定

由于尺度数P=2，因此WANN模型需要构造P+1=3个BP神经网络。从图7.14可以清楚地看出，八五三农场的地下水埋深动态变化规律具有明显的周期特征（周期为1年），因此，为了使这种周期特性在网络中能够有所反映，可采用前i个点值来得到第i+1个点值的方法。本节分别选取小波分解序列W1（t）、W2（t）和C2（t）前12个月的数据作为网络输入，当月的1个数据作为网络输出，将八五三农场14年的各小波分解序列（均包含168个数据）分别生成156个样本对。

3.WANN模型结构的确定

如前所述，3个BP神经网络的输入层节点数为12，输出层节点数为1。隐层节点数可根据式（7.18）进行调试。经过试错，本节选定隐层节点数ni=12。因此，本节设计的WANN模型中各BP神经网络的拓扑结构为12∶12∶1。

4.WANN模型拟合

采用MATLAB7.0编程并运行程序，对WANN模型训练3000次。采用小波重构算法将各BP神经网络的拟合结果进行叠加，即可得到WANN模型的拟合值，拟合结果如图7.15所示。

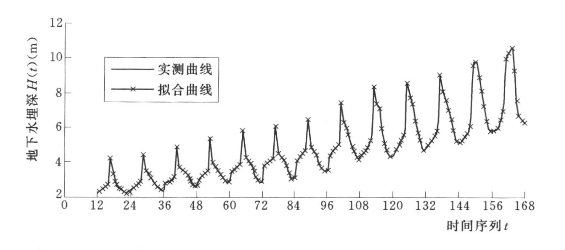
图7.15　八五三农场逐月地下水埋深WANN模型拟合曲线(www.xing528.com)

5.WANN模型精度检验

采用所建WANN模型的拟合数据进行拟合效果检验，并采用未参加建模的2005年逐月地下水埋深实测数据进行试报效果检验，具体计算结果见表7.5。

表7.5　WANN模型精度检验结果

根据有关文献可知，各项指标均达到1级标准（陈南祥，1999）。因此，所建八五三农场地下水埋深WANN模型拟合效果良好，预测精度较高，可用于预测八五三农场未来地下水埋深。

6.地下水埋深预测

现采用已经训练好并经过精度检验的WANN模型预测2006～2009年八五三农场逐月地下水埋深，地下水埋深预测值及预测曲线分别见表7.6和图7.16。

表7.6　八五三农场逐月地下水埋深WANN模型预测值（2006～2009）　单位：m

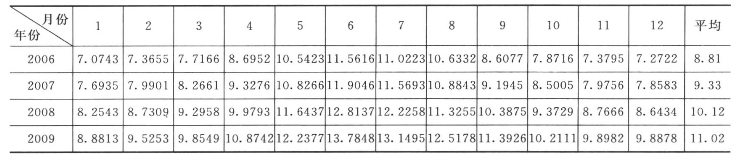
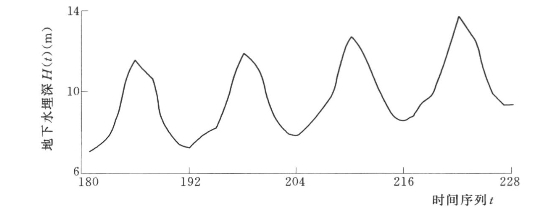
图7.16　八五三农场逐月地下水埋深WANN模型预测曲线（2006～2009）

从表7.6和图7.16中可以看出，如果仍然采用过去的地下水开采模式，八五三农场的地下水位将会持续下降，而且降幅会越来越大。2006～2009年地下水埋深年降幅分别为0.42m、0.52m、0.79m和0.90m，未来4年地下水埋深平均年降幅为0.66m左右。因此，为了保护八五三农场有限的地下水资源，应加强科学管理，严格控制地下水开采。