八五三农场地下水动态变化的时间序列模型预测

八五三农场位于黑龙江省三江平原东部，隶属于黑龙江省农垦总局红兴隆分局，土地总面积1165.7km2，其中耕地面积581.35km2。八五三农场是一个以种植麦、豆、玉米、水稻为主的大型机械化国营农场，1991年开始种植水稻，面积仅为0.61万hm2，到2000年，水田面积激增到2.67万hm2。据调查，八五三农场多年平均地下水可开采资源量为0.4121亿m3/a，而2000年地下水开采量为0.8046亿m3/a（井灌水稻面积为1.91万hm2），已经出现了严重的地下水超采现象，　“吊泵”现象大量出现。按此趋势发展下去，必然会对当地的工农业生产和居民用水产生严重威胁。因此，本节根据红兴隆分局水务局提供的八五三农场1991～2004年的逐月地下水埋深实测序列资料（n=14×12=168个月）建立地下水埋深时间序列模型，将2005年的逐月地下水埋深实测序列资料作为预留检验，对当地地下水埋深动态进行模拟和预测，为当地地下水的科学管理提供参考依据。

根据实测序列资料绘制八五三农场地下水埋深动态变化曲线，如图7.1所示。从图7.1可以看出，八五三农场的逐月地下水埋深呈逐渐增大的趋势。从1991～1998年8年间，地下水埋深增加了2.1m，地下水位年平均降幅为0.3m/a，这是由于这段时间内水田面积一直维持在15万亩左右，地下水开采量不大，所以导致地下水位缓慢下降。而从1999年开始，随着外来水稻承包户的增多，水田面积迅速增加，截止2000年，水田面积发展到40万亩，增长了1倍多，所以导致地下水位降幅增加，1999～2004年6年间，地下水位年平均降幅为0.7m/a左右。地下水位的持续下降已经严重地破坏了当地地下水资源的供需平衡。从图7.1中还可以看出，由于季节性降水的影响，使得地下水埋深的动态变化具有明显的以年为周期的变化规律。因此八五三农场1991～2004年的逐月地下水埋深数据序列可以采用上述方法进行时间序列分析。

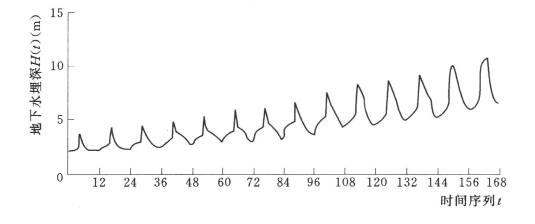
图7.1　八五三农场地下水埋深动态变化曲线（1991～2004）

7.1.2.1　建立趋势项模型

在显著性水平α=0.05的情况下，挑选出适宜的趋势项模型为：

根据趋势项模型，绘制趋势项曲线见图7.2。

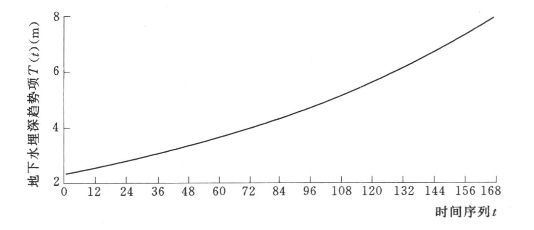
图7.2　八五三农场地下水埋深趋势项曲线

采用Mann-Kendall方法对剩余序列H（t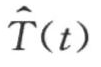）-进行突变性检验。经过编程计算，剩余序列无显著突变点，不含突变项。

7.1.2.2　建立周期项模型

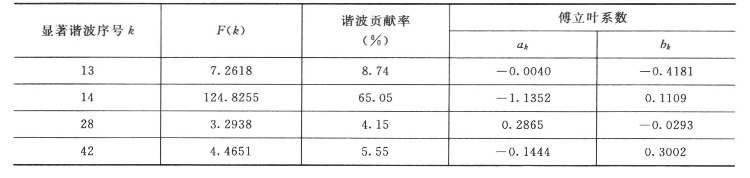
样本数n=168，则谐波数L=84。按照上述方法，经过计算得到序列y（t）的总方差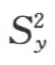=1.0804，均值a0=0.0770。在显著性水平α=0.05时，Fα=3.05（n1=2，n2=165）。通过编程计算，达到显著性水平的谐波序号为13、14、28、42，计算结果见表7.1。

表7.1　显著性检验计算结果

所以，周期项模型为：

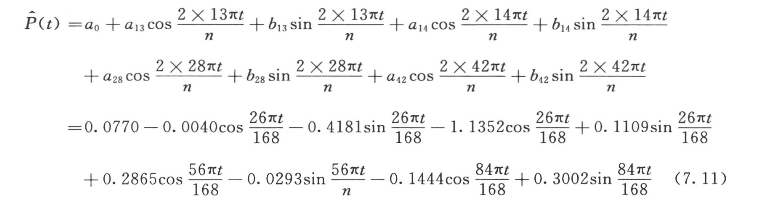
根据周期项模型绘制周期项曲线，如图7.3所示。

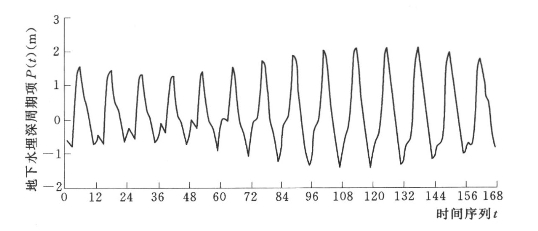
图7.3　八五三农场地下水埋深周期项曲线

7.1.2.3　建立随机项模型

1.正态性检验

经过计算，随机序列R（t）的均值为R（t）=3.2729×10-5，趋近于0，方差为S2=0.2406，偏态系数CsR=0.0699，趋近于0，所以认为随机序列R（t）为正态分布，不必进行正态性转化。

2.自相关分析

样本数n=168，取最大时移m=84。编程计算随机序列R（t）的自相关系数，并绘制自相关图，在自相关图上加绘置信水平为95%（显著性水平α=0.05）的容许限，如图7.4所示。由自相关图可见，第4阶、12阶、24阶、36阶、48阶均显著异于随机序列，因此地下水年际变化具有相依性，为一组相依序列，可以选用AR（p）模型。

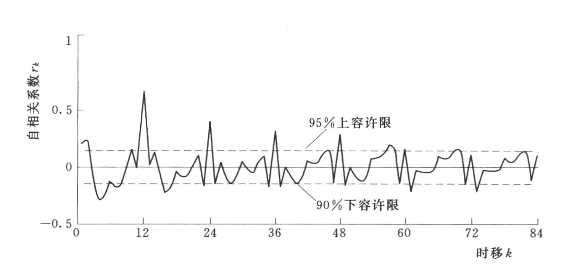
图7.4　八五三农场地下水埋深随机序列自相关图

3.偏相关分析

偏相关分析的主要任务是确定AR（p）模型的阶数。采用尤尔——沃尔克估计法，编程计算随机序列R（t）的偏相关系数φk，并绘制偏相关图，在偏相关图上加绘置信水平为95%的容许限，如图7.5所示。由偏相关图可以看出，当k≥12时，φk，k基本落入95%容许限范围内，因此，可以初步确定AR（p）模型阶数为12阶。选定k=1，4，11，12（偏相关系数超出95%容许限范围），则随机序列相依成分AR（p）模型为：

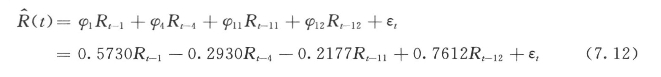(www.xing528.com)

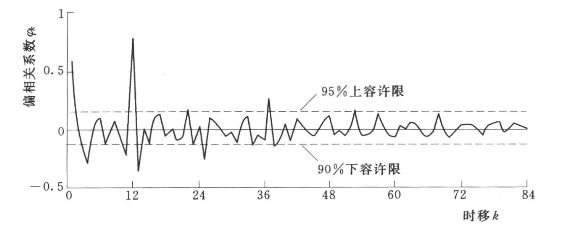
图7.5　八五三农场地下水埋深随机序列偏相关图

4.AR（p）模型的进一步识别

模型阶数p初步确定后，还需要采用AIC准则或BIC准则进一步识别AR（p）模型的阶数是否合适。本节采用BIC准则。通过编程计算，p=12时，BIC达到最小值，BIC（12）=168ln0.0643+12ln168=-399.5373。这说明，初步确定的模型阶数为12阶是合适的。

5.模型检验

AR（p）模型检验主要是检验残差项εt是否为独立序列。本节采用自相关系数综合检验法，经过计算，统计量Q=17.9256，n=168，取m=n/4=168/4=42，查χ2表得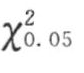=43.773，Q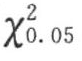＜，所以εt为独立随机序列。

对独立随机序列εt的正态性进行检验：均值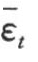=-0.0025→0，方差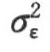=0.1281，偏态系数Cs（e）=-8.9749×10-4→0，因此通过检验，εt～（0，0.1281）正态分布。因此，随机项模型为：

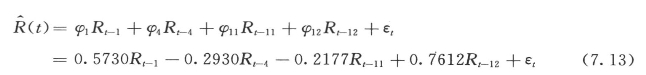
根据随机项模型绘制随机项曲线，如图7.6所示。

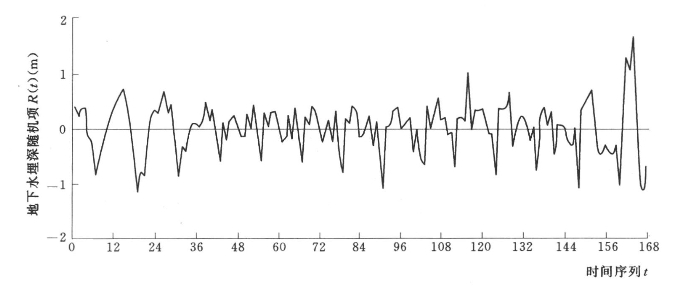
图7.6　八五三农场地下水埋深随机项曲线

分别采用长序列法和短序列法（丁晶，1997）对所建立的随机项AR（12）模型进行实用性分析。经过编程计算，结果表明：模拟序列无法保持原序列R（t）的均值、方差、偏态系数、一阶自相关系数等主要统计特征。考虑到此处建模的目的仅仅是为了预报地下水埋深，因此，只要后续的模型精度检验符合要求，所建的AR（12）模型即通过实用性检验。

6.模型组合

将趋势项、周期项和随机项模型叠加，就可以得到地下水埋深动态变化预测模型，即

7.模型拟合

采用建立的地下水埋深时间序列预测模型对八五三农场1991～2004年的逐月平均地下水埋深进行拟合，如图7.7所示。

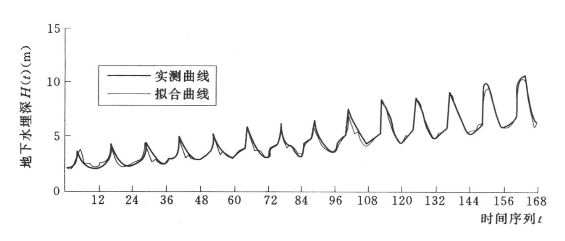
图7.7　八五三农场地下水埋深时序模型拟合曲线

8.模型精度检验

经过计算，拟合效果评价指标后验差比值C=0.1166，小误差频率p=1，相对均方误差E1=6.92%，拟合准确率E2=0.976，其中，C、p、E2均达到1级标准，E1达到2级标准（陈南祥，1999）。从图7.7中可以看出八五三农场地下水埋深时序模型拟合效果良好。

采用未参加建模的2005年地下水埋深实测数据进行试报效果检验，经过计算，试报效果指标E3=100%，达到1级标准。因此，所建的地下水埋深时间序列预测模型可靠性和预测精度较高，可用于预测八五三农场未来地下水埋深。

9.地下水埋深预测

现依据经过精度检验的地下水埋深时序模型预测2006～2009年八五三农场逐月地下水埋深，地下水埋深预测值及预测曲线分别见表7.2和图7.8。

表7.2　八五三农场逐月地下水埋深时序模型预测值（2006～2009）　单位：m

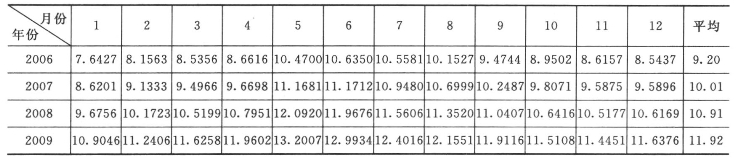
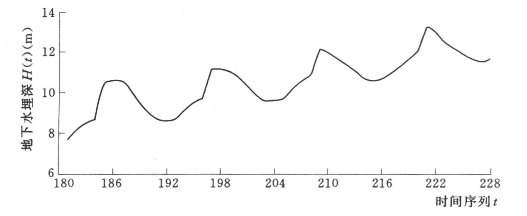
图7.8　八五三农场2006～2009年地下水埋深时序模型预测曲线

从表7.2和图7.8中可以看出，如果继续采用过去的地下水开采模式，必然会导致八五三农场地下水位的持续下降，而且降幅会越来越大。2006～2009年地下水埋深年降幅分别为0.81m、0.81m、0.90m和1.01m，未来4年地下水埋深平均年降幅为0.88m左右。因此，为了保护有限的地下水资源，八五三农场必须严格控制地下水开采，加大科学管理力度，防止地下水位继续下降而导致当地生态环境的恶化。