八五三农场年降水序列多时间尺度变化特征分析

现以八五三农场为例，根据上述小波分析理论，对八五三农场年降水实测序列资料进行多时间尺度分析，以了解其不同时间尺度下的详细结构和变化趋势。

5.5.2.1　资料来源及处理

从红兴隆分局气象台收集到八五三农场1959～2005年的全年降水资料（n=47）。为处理方便，将年降水实测序列资料进行距平（中心化）处理，并绘制年降水距平序列变化曲线，如图5.19所示。

5.5.2.2　年降水距平序列小波变换

按照前述方法，编程计算八五三农场年降水距平序列f（kΔt）（k=1，2，…，47；Δt=1）的小波变换系数Wf（a，b）。

由于Morlet小波属于复数小波，因此其小波变换系数包括实部和虚部两个部分。参考相关文献可知，小波变换的模平方与函数f（t）在其小波变换域中的能量成正比，|Wf（a，b）|2就是信号在a、b时的小波频谱能量，因此小波变换模平方就可以用来表示特征时间尺度信号能量的强弱（崔凤林等，2000；张少文等，2004；Mi X C et al，2005）。而不同特征时间尺度信号在不同时间上的分布和位相两方面的信息则可以用小波变换的实部来表示。因此，年降水距平序列小波变换系数Wf（a，b）的模平方和实部就蕴含着序列随着时间尺度a（即周期T）和时移b而变化的特征信息。

5.5.2.3　年降水距平序列时频分析

图5.19　八五三农场年降水距平变化曲线（1959～2005）

按照前述方法绘制八五三农场年降水距平序列小波变换系数Wf（a，b）的模平方等值线图（图5.20）和实部等值线图（图5.21），在此基础上进行年降水距平序列的时频变化分析。

图5.20　八五三农场年降水距平序列小波变换系数模平方（×104）等值线

1.小波变换系数模平方时频特性分析

由图3.20可以看出不同时间尺度信号能量分布的强弱，其中2～4年时间尺度信号能量变化最强，主要发生在1978～1996年，振荡中心在1981年；4～12年时间尺度信号能量变化也较强，主要发生在1959～1988年，振荡中心在1971年；25～37年时间尺度信号主要发生在1959～2000年；1～2年时间尺度信号主要发生在1959～1961年、1968～1973年、1974～1977年、1982～1985年、1987～1993年；其余时间尺度信号能量变化则较弱。

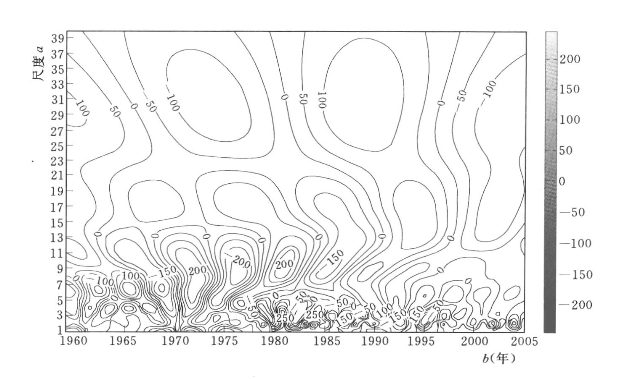
图5.21　八五三农场年降水距平序列小波变换系数实部时频分布

2.小波变换系数实部时频特性分析

由图5.21可以看出不同时间尺度的变化、正负位相转变点的分布及其位相结构，其中，1～4年、4～12年、25～37年时间尺度表现最为明显，正负位相交替出现，其中心时间尺度为3年、7年和30年左右。另外，12～21年时间尺度也有表现，其中心时间尺度为17年左右。为了进一步说明八五三农场年降水距平序列旱、涝交替变化的波动特性，在图5.21上固定时间尺度a值（分别取a=3、7、17、30），作平行于b轴的切割线，在切割线上取点，作小波变换系数Wf（a，b）的实部，表示为R［Wf（a，b）］，随时移b变化的过程线，如图5.22所示。

图5.22　不同尺度下年降水距平序列Morlet小波变换实部变化过程(www.xing528.com)

图5.22（a）给出了3年时间尺度小波变换系数实部变化过程，降水量旱涝变化及正负位相转变点位置可以准确给出（限于篇幅，这里不具体给出）。图5.22（b）给出了7年时间尺度小波变换系数实部变化过程，可以看出，1960年以前、1964～1967年、1971～1974年、1978～1982年、1987～1990年、1994～1996年、2000～2002年为正位相，表示降水量偏多；而1961～1963年、1968～1970年、1975～1977年、1983～1986年、1991～1993年、1997～1999年及2003年以后为负位相，表示降水量偏少；正负位相转变点在1961年、1964年、1967年、1970年、1974年、1978年、1982年、1987年、1990年、1994年、1997年、2000年和2003年。图5.22（c）给出了17年时间尺度小波变换系数实部变化过程，可以看出，1963年以前、1973～1981年、1990～1998年为正位相，表示降水量偏多；而1964～1972年、1982～1989年及1999年以后为负位相，表示降水量偏少；正负位相转变点在1964年、1972年、1981年、1990年和1998年。图5.22（d）给出了30年时间尺度小波变换系数实部变化过程，可以看出，1965年以前和1981～1996年为正位相，表示降水量偏多；而1966～1980年及1997年以后为负位相，表示降水量偏少；正负位相转变点在1966年、1981年和1996年。

5.5.2.4　年降水序列主要周期分析

利用已经求解出来的不同尺度下的小波变换系数，按照前述方法，通过计算机编程，绘制八五三农场年降水距平序列小波方差图，如图5.23所示。从图5.23可以看出，小波方差的主要峰值分别出现在尺度a=3、7、17、30处，第一峰值为尺度a=3所对应的小波方差，说明3年左右的周期振荡最强，为第一主周期，第二、第三、第四主周期分别为7、30和17年。为了识别上述主周期是否具有统计意义，还需要进行显著性检验。

小波方差是否显著，可以采用红噪声或白噪声标准谱进行检验（Torrence C et al，1998；郝立生等，2007）。若原序列滞后1的自相关系数r（1）＞0.1，则用红噪声谱检验；若r（1）≤0.1，则令r（1）=0，用白噪声谱检验。具体检验公式如下：

式中　Pa——红噪声或白噪声标准谱；

r（1）——原序列滞后1的自相关系数；

Δt——原序列时间间隔。

式中　P——小波理论功率谱；

σ2——原序列方差；

——显著性水平α=0.05、自由度为ν时的χ2分布值，其中：

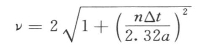
若Var（a）＞P，则说明小波方差所对应的周期是显著的。

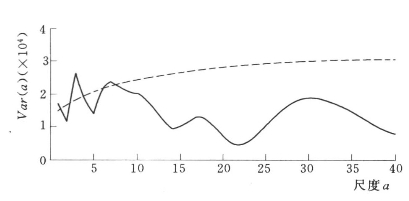
图5.23　八五三农场年降水距平序列小波方差（实线为小波方差，虚线为95%置信水平）

经过计算，八五三农场年降水序列的一阶自相关系数r（1）=0.0481＜0.1，所以采用白噪声谱对小波方差进行检验，如图5.23所示。由图5.23可以看出，只有3年和7年左右的周期超过了95%置信水平，因此，八五三农场年降水序列真正的主周期为3年和7年左右。17年和30年左右的小波方差虽然也具有一定峰值，但已不明显。

5.5.2.5　年降水序列变化趋势分析

图5.22已经给出不同尺度下小波变换系数实部变化过程，通过图5.22即可分析出各主要时间尺度下八五三农场年降水序列的变化趋势。分析较小尺度3年和7年以及较大尺度17年的变化趋势可以看出，2006～2007年左右，八五三农场的年降水量将处于偏少期，而2008年以后将进入降水偏多期；分析较大尺度30年的变化趋势可以看出，2006～2011年左右，八五三农场的年降水量将处于偏少期，而2012年以后的15年内，八五三农场的年降水量将处于偏多期。