1.小波函数
小波函数是指具有震荡特性、能够迅速衰减到零的一类函数，即
。小波函数有多种，在小波分析中经常采用Marr小波、Morlet小波、Wave小波等（Ippolitov et al，2002；欧素英等，2004；刘忠阳等，2005；王文圣等，2005）。本节选用在时域和频域局部性都较好的Morlet小波，其函数为：
式中 c——常数；
i——虚数。
Morlet小波是由一个周期函数经过Gaussian函数平滑而得到的，所以它的尺度因子a与Fourier变换中的周期有一一对应的关系：
。当取常数c=6.2时，T=1.00057a≈a，所以Morlet小波可以用来进行周期分析。
2.小波变换
小波变换是小波分析的核心。对于给定的满足一定条件的小波函数ψ（t），时间序列f（t）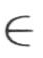
L2（R）的连续小波变换定义为（吴东杰等，2004；刘忠阳等，2005；王文圣等，2005）：
式中 Wf（a，b）——小波变换系数；
a——尺度因子，反映小波的周期长度；
b——时间因子，反映时间上的平移。(www.xing528.com)
在实际应用中，水文时间序列大多是离散的。例如f（kΔt）（k=1，2，…，n；Δt为取样时间间隔），则式（5.13）的离散形式为（Ippolitov I I等，2002；吴东杰等，2004；刘忠阳等，2005；王文圣等，2005；Subasi A et al，2005）：
Wf（a，b）能同时反映时域参数b和频域参数a的特征，它是时间序列f（t）或f（kΔt）通过单位脉冲响应的滤波器的输出。当a较小时，对频域的分辨率较低，而对时域的分辨率较高；当a较大时，对频域的分辨率较高，而对时域的分辨率较低。因此，小波变换能实现窗口的大小固定、形状可变的时频局部化。
根据Wf（a，b）随a和b的变化，可以绘出以b为横坐标，a为纵坐标的关于Wf（a，b）的二维等值线图，称为小波变换系数图。通过分析小波变换系数图，可以得到水文时间序列在小波变换域中的小波变化特征，从而揭示出水文时间序列的多时间尺度演变特征和突变特征。
3.小波方差
将时间域上关于a的所有小波变换系数的平方进行积分，即为小波方差。对于离散水文时间序列，小波方差可以采用下式（Mi X C et al，2005；刘建梅等，2005）计算：
式中 n——样本数；
|Wf（a，b）|2——小波变换系数模平方。
小波方差随尺度a变化的过程，称为小波方差图，该图能反映水文时间序列中所包含的各种尺度（即周期）的波动及其强弱（能量大小）随尺度变化的特性，图中各个峰值分别对应着各个显著周期。因此，通过小波方差图可以很方便地确定一个时间序列中存在的主要时间尺度（即主周期）。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
