湖泊水质模型-《水资源保护理论与实践》成果

3.1.2.1　完全混合水质模型

对于面积小，封闭性强，四周污染源多的小湖或湖湾，污染物入湖后，在湖流和风浪作用下，与湖水混合均匀，湖泊各处污染物浓度均一。

对完全混合型的湖泊，根据物质平衡原理——某时段任何污染物含量的变化等于该时段流入总量减去流出总量，再减去元素降解或沉淀等所损失的量，建立数学方程如下：

对难降解的污染物为：

式中　Mt——时段末湖泊内污染物总量；

M0——时段初湖泊内污染物总量；

M——时段内湖泊平均污染物总量；

Δt——计算时段；

ρ、ρ'——时段内平均流入、流出湖泊污染物总量速率；

K——污染物衰减率。

1.湖泊营养物积存过程的水质模型

营养物积存过程的水质模型：

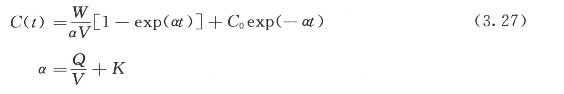
式中　V——湖泊容积；

Q——流入湖泊的流量；

K——营养物降解和沉淀率；

C、C0——湖水营养物的浓度和初始浓度；

W——营养物入流量。

当营养物入流量W（t）不同时，则C（c）也不一样。当W（t）为常量时，即W（t）=W0，则：

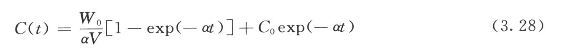
当W（t）呈线性变化时，即W（t）=W0±ωt，则：

当W（t）呈指数变化时，即W（t）=W0exp（±ωt），则：

当W（t）呈极限型变化时，即W（t）=W0［1-exp（-ωt）］，则

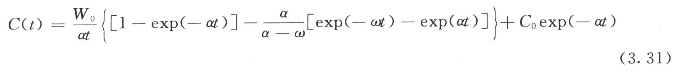
2.出入湖水量相等的水质模型

当出入湖水量相等，单位时间内，湖泊内污染物蓄量变化方程为：

湖水污染物浓度模型为：

式中　T——滞留时间；

V——湖泊容积；

Q——出入湖泊流量；

C1、C0——入湖水中污染物浓度和湖水初始污染物浓度。

3.出入湖水量不相等的水质模型

当出入湖水量不相等时，则单位时间内，湖泊污染物蓄量变化方程为：

湖水污染物浓度模型为：

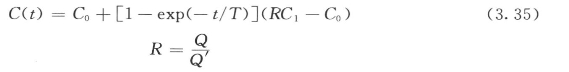
式中　Q、Q'——流入和流出湖泊的流量；

其他符号意义同前。

4.湖泊蓄盐量的水质模型

式中　M2、M1——计算时段末和初湖泊内贮盐量；

Q、Q'——入湖和出湖水量；

C1、C——入湖和出湖水中离子浓度；(www.xing528.com)

S——湖泊内贮盐量的衰减量。

5.湖泊溶氧模型

湖水中溶解氧变化为入湖水量增氧，空气复氧增氧和各种因素耗氧、减氧的总和，湖泊溶氧平衡方程为：

式中　C——湖水溶氧度；

C1——入湖水中溶氧浓度；

Cs——饱和溶氧浓度；

V——湖泊容积；

Q——入湖流量；

k2——湖水复氧系数；

R——湖泊内生物和非生物因素耗氧总量。

3.1.2.2　非完全混合水质模型

对于水域宽阔的大湖泊，当污染物流入湖泊后，污染仅出现在排污口附近的水域。这时需要考虑污染物在湖水中稀释、扩散规律，采用不均匀混合水质模型描述。

1.湖泊扩散的水质模型

对难降解污染物，当排污稳定，且边界条件为r=r0时，C=C0，则得：

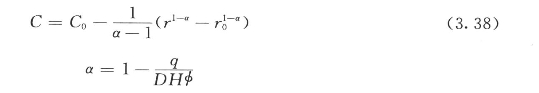
式中　r——距排污口距离，如图3.2所示；

q——入湖污水量；

C——r处污染物浓度；

H——污染物扩散区平均湖水深；

φ——污染物在湖水中的扩散角，如排污口在垂直的湖岸，φ=180°；

C0——距排污口为r0处污染物浓度；

D——湖水紊动扩散系数（因湖泊中风浪的影响）。

D的计算式为：

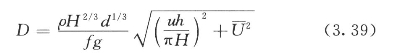
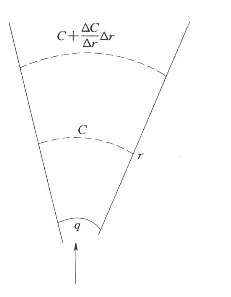
图3.　2污染物在湖水中扩散示意图

式中　ρ——水的密度；

d——湖底沉积物的颗粒直径；

f——经验系数；

g——重力加速度；

u——流速；

h——波高；

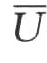——风生流和梯度流合成的平均流速。

2.湖泊自净的水质模型

当忽略扩散项，排污是稳定的，湖水中污染物浓度递减。当r=r0时，C=C0，则得湖泊自净的水质模型：

式中　K——污染物白净速率常数；

C0——排污口污染物的浓度；

其他符号意义同前。

3.湖泊氧亏模型

湖泊氧亏模型为：

式中　D——距排污口r处的湖水的氧亏量；K1——耗氧速率常数；

K2——复氧速率常数；

BOD0——排污口的生化需氧量；

D0——排污口的氧亏量。