水质模型在水资源保护中的应用

3.1.1.1　均匀混合水质模型

当污染物进入河段后，假设完全混合均匀，根据物质平衡原理，可建立水质模型基本方程如下：

1.稳态情况

当污染物进入河段后，其浓度不随时间变化而变化时，称均匀混合的稳态情况，即

将此条件代入式（3.1），解为：

如果是连续河段，则第i河段模型为：

式中　C0——起始断面污染物浓度；

K——污染物衰减系数；

V——河段水体体积；

Q——河段流量；

Δx——河段长度；

u——河段流速。

2.非稳态情况

当污染物进入河段后，起浓度随时间变化而变化时，称为非稳态混合情况。将式（3.1）整理得：

在t=0、C=C0、t=t、C=C时，求解得：

式中　C0——起始断面浓度；

I——污染负荷函数，即单位水体污染物输入速率，

θ——水力停留时间，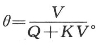

3.1.1.2　一维水质模型

如果污染物进入河段后，其浓度只沿水流方向（x轴向）变化，在垂直于水流方向的y、z轴向上浓度是均匀的，且污染物的降解服从一级反应，这时河流污染物变化可用一维水质模型描述。河流一维水质模型基本方程为：

对难降解的污染物，K=0，则基本方程为：

式中　C——河水污染物浓度；

Ex——纵向（顺河水流向）离散系数；

u——断面平均流速；

K——污染物衰减系数；

t——时间；

x——纵向（顺河水流向）距离。

1.稳态模型

当污染物输入量、断面平均流速和纵向离散系数不随时间变化时，则河水污染物浓度是稳定的，即，边界条件当x=0时，C=C0；当x=∞时，C=0。

易降解污染物一维稳态模型的解析解为：

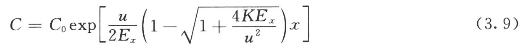
难降解污染物一维稳态模型的解析解为：

如果忽略离散作用，河流一维稳态模型的解析解则为：

式中　C0——x=0处河水中的污染物浓度；

其他符号意义同前。

2.非稳态模型

（1）瞬时源。初始和边界条件为：

C（x，0）=0（x≥0）

C（0，t）=C0（t＞0，t→0）

瞬时源以为非稳态模型的解析解为：

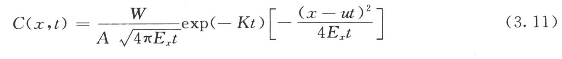
难降解污染物瞬时源以为非稳态模型的解析解为：

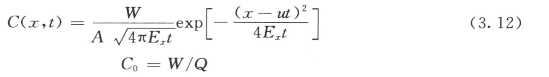
式中　C——x处t时刻和水污染物浓度；

C0——起始断面污染物浓度；

W——瞬时排放的污染物总量；

A——河流断面面积；

u——断面平均流速；(www.xing528.com)

Ex——纵向离散系数；

Q——河水流量；

t——时间；

K——污染物衰减系数。

（2）连续源。初始和边界条件为：

C（x，0）=0 x≥0

C（0，t）=C0 t＞0

连续源非稳态模型的解析解为：

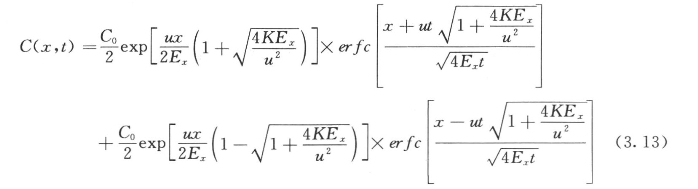
难降解污染物连续源非稳态模型的解析解为：

式中　C0——起始断面污染物浓度；

erfc（x）——余误差函数

u——河流纵向距离；

C——x处t时污染物浓度；

Ex——纵向离散系数；

K——污染物衰减系数。

3.1.1.3　二维水质模型

在宽浅河流上，排入河中的污染物，在水深方向（z轴向）可以认为混合均匀，在水平面的纵向（y轴向）和横向（x轴向）形成混合区，且污染物的降解服从一级反应，这时河水的水质需用二维水质模型描述。在稳态情况下二维水质模型基本方程为：

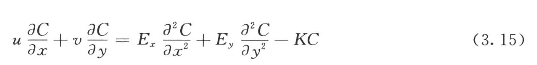
式中　C——污染物浓度；

x——沿河水流向的坐标；

y——垂直工轴的横向坐标；

u——河水纵向流速；

v——河水横向流速；

Ex、Ey——纵向和横向离散系数；

K——污染物衰减系数。

二维水质模型基本方程，一般只能用数值法求解。在最简单的情况下，才有解析解。

二维随之模型最简单的情况是在无限宽的河段中x=0及y=0处有一单个点源——无限边界单点源模型；此外还有河岸影响的点源模型等。

3.1.1.4　溶解氧模型

河水中的溶解氧数量是反映河流污染程度和水环境质量的一个重要的指标。同时，溶解氧与水污染和水环境质量的许多参数密切相关。因此，溶解氧模型得到广泛应用和发展。下面介绍一种最基本的溶解氧模型：斯特里特—费尔普水质模型（简称S—P模型）。

1925年，美国两位工程师（斯特里特和费尔普）根据俄亥俄河的污染调查研究，认为在河流的自净过程中，同时存在两个过程：有机污染物进行生物氧化，消耗水中溶解氧，其速率与水中有机污染物浓度成正比；大气中的氧不断地进入水体，即所谓大气复氧，其速率与水体的氧亏值（即水中溶解氧的实际浓度与该水温条件下氧的饱和溶解度之差）成正比。根据质量守恒原理，若考虑断面流速与污染物浓度分布不均匀而产生的纵向离散作用，则氧平衡的微分方程为：

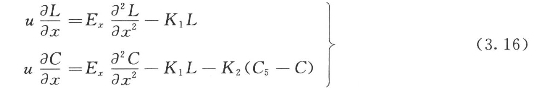
式（3.16）称为S—P模型微分式的托曼修正式。

将起始和边界条件代入式（3.16），解得S—P模型积分式的托曼修正式为：

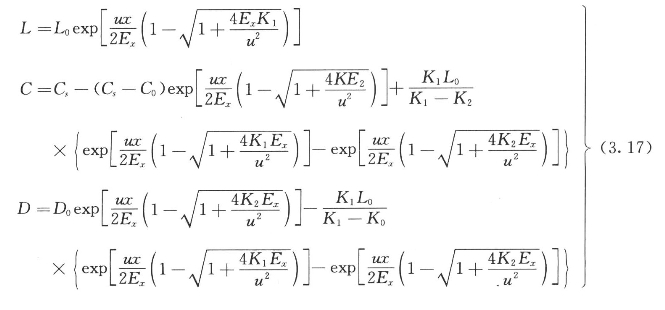
若忽略离散作用，则得S—P模型的微分式为：

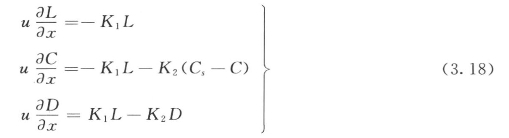
将起始和边界条件代入式（3.18），解得S—P模型的积分式：

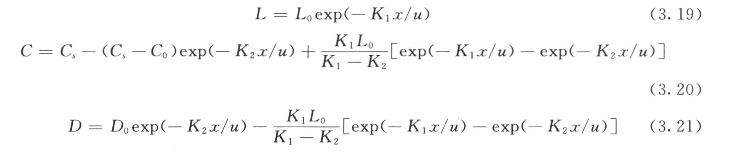
式中　L、L0——x=x和x=0处河水生化需氧量浓度；

C、C0——x=x和x=0处河水溶解氧浓度；

D、D0——x=x和x=0处河水溶解氧的氧亏浓度；

Cs——河水某温度下的饱和溶解氧；

x——顺河水流动方向的纵向距离；

u——河水平均流速；

K1、K2——耗氧系数和复氧系数；

Ex——纵向离散系数。

S—P模型是描述污染物进入河流水体之后，耗氧过程和大气复氧过程的平衡状态。溶解氧在河水中变化为一下垂曲线，称氧垂曲线，如图3.1所示。溶解氧浓度有一个最低值，称为极限溶解氧Cc。出现Cc的距离称为极限距离xc。

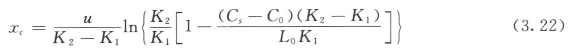
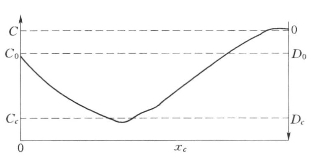
图3.1　溶解氧沿河变化图

极限溶解氧：

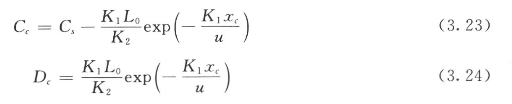
式中　Dc——极限氧亏；

其他符号意义同前。