河流水质模拟：水资源保护实践

水质预测是水环境规划、评价和管理工作的基础。实现河流水质的高效预测对促进水资源的可持续利用具有重要的现实意义。河流水质的预测是根据已有的河流水质观测资料，通过分析处理，利用已知量寻求未知量的过程。灰色系统分析方法对于信息不完整或不完全的实际情况具有良好的适用性，其中的GM（1，1）模型在水质预测中得到了较为广泛的运用，但多属于单一灰色GM（1，1）预测模型形式，对于具有周期性波动趋势的水质进行预测，则精度不高。采用实时在线、灰色新陈代谢GM（1，1）对河流水质动态进行了预测分析，明显地提高了预测精度。

2.6.1.1　灰色新陈代谢模型的建模

1.常规GM（1，1）模型

建立GM（1，1）模型的实质是对原始数据作一次累加生成，使生成数据呈一定规律，通过建立微分方程模型，求得拟合曲线，用以对系统进行预测。

对于给定的原始时间序列｛x（0）（t）=x（0）（1），x（0）（2），…，x（0）（n）｝做一次累加生成1-AGO：｛x（1）（t）=x（1）（1），x（1）（2）…，x（1）（n）｝，其中n作x（1）的一阶均值生成：x=［x（2），（3），…x（n）］，其中1）］，t=2，3，…，n其相应的微分方程为，利用最小二乘法求解参数a，u：

其中

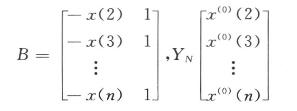
式中　B——累加生成矩阵；

YN——数据向量。

时间响应函数离散化得x（1）的GM（1，1）模型为：

x（0）的灰色预测模型：(www.xing528.com)

为判别模型优劣，可使用后验差检验，模型精度检验过程如下：

令ek=x（0）（k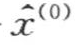）-（k）（k=1，2，…，n）第k个数据的相对误差Δk=|ek/x（0）（k）|原始数据均值；原始数据方差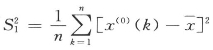；残差均值；残差方差；相对误差检验后验差比值检验c=S2/S1；小误差概率检验

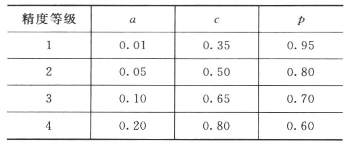
一个系统预测模型的好坏，只有经过全面精度检验与评价，才能真正符合实际条件。模型精度检验的指标见表2.1。

表2.1　精度检验等级参照表

2.新陈代谢GM（1，1）建模方法

在实际建模过程中，特别是在时间上连续、不断有新的建模数据产生的实际系统中，原始数据序列的数据不一定全部用来建模，只需从中取出一部分数据，就可以建立一个模型，再根据系统产生的最新数据，去掉原系统中最陈旧的数据，重新建立GM（1，1）模型，这样在不断补充新信息的同时，及时去掉老数据，建模序列更能反映系统在目前的特征。在灰色新陈代谢模型中，构成其模型的原始数据序列中的数据个数，最少不能少于4个。在实际建模中，也并非是原始数据序列的全部数据都用来建模就是最理想的，而是要视其模拟精度来选取。用实时在线方法，建立等维（n=6）新陈代谢模型对河流水质进行预测。

2.6.1.2　灰色新陈代谢GM（1，1）模型优点

（1）灰色新陈代谢GM（1，1）用于河流水质预测，符合水环境的灰色性，模型适用性好，与环境状况相吻合。

（2）灰色新陈代谢模型能够及时补充新的信息而去掉因时间推移而使信息意义降低的老信息，因而它能反映系统当前特征，比常规的GM（1，1）模型更能接近实际。

（3）该模型对其他具有时间连续性的非单调递增或递减函数序列的预测具有重要的参考价值，应用前景是十分广阔的。