消落带藻华形成机制及综合影响模型研究

在上述各水文水质指标、营养盐指标、金属离子及酶活性指标中，与藻密度具有内在联系，同时具有显著相关性的指标包括V、pH、Chla、Zn2+、POC、CO2、SRP、EHP、CAA、NRA、APA。在上述内容中从各个指标的角度阐述了其与藻密度之间的联系，然而由于藻类的生长影响因素十分复杂，从单个指标无法较为全面地阐述藻类的生长规律及藻华的成因。因此有必要建立藻密度综合影响模型，将上述参数引入模型，从而更加全面地描述嘉陵江主城段藻类的生长规律。由于上述指标间存在一定的相关性，为避免共线性的发生，增加模型的可信度，本书将通过主成分回归的方法将各指标引入模型，从而建立藻密度综合影响模型[187]。

表4.6　主成分解释的总方差

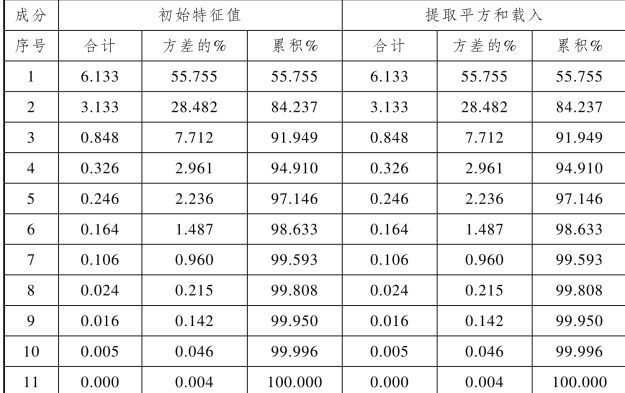
通过SPSS主成分分析，我们得到了各主成分的特征值及其解释的总方差百分比（见表4.6）。如表4.6所示，成分1与成分2特征值均大于1，同时二者可解释84.237%的总方差。当主成分所解释的累积方差大于80%时，即可提取相应主成分，因此本书将提取2个主成分进行进一步分析。

如图4.18所示为所提取的主成分所含各参数的得分图，如表4.7所示为主成分与各参数间的得分矩阵，主成分1和主成分2分别记为C1（Component 1）、C2（Component 2）。

表4.7　成分矩阵

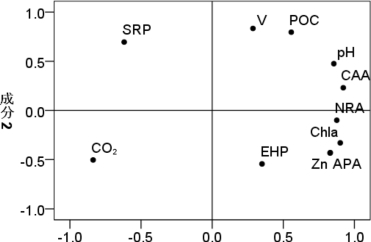
图4.18　嘉陵江藻密度相关指标主成分得分图

通过各参数的得分结合主成分的特征值，可以计算出主成分中各指标的系数，计算公式如下：(https://www.xing528.com)

将各成分得分及特征值代入公式（4.3），经计算求得各指标在主成分中的系数，从而得到主成分与各指标间的关系式如下：

C1＝0.116V＋0.345pH＋0.335Zn2+＋0.363Chla－0.225POC－0.338CO2－0.25SRP＋0.141EHP＋0.354NRA＋0.335APA＋0.372CAA；

C2＝0.471V＋0.268pH－0.245Zn2+－0.186Chla＋0.45POC－0.285CO2＋0.393SRP－0.307EHP－0.056NRA－0.242APA＋0.13CAA。

对C1、C2与藻密度进行线性拟合，得到主成分回归系数，如表4.8所示。

表4.8　主成分回归系数

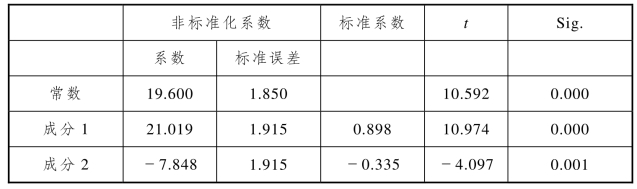
藻密度与主成分间的关系式为：Cells＝21.019C1－7.848C2＋19.6（R2＝0.906）。将各主成分与指标间的关系式代入，得到藻密度与各指标间的关系式：Cells＝－1.262V＋5.152pH＋8.962Zn2+＋9.103Chla＋1.191POC－4.871CO2－8.336SRP＋5.383EHP＋7.88NRA＋8.948APA＋6.807CAA＋19.6。此关系式为嘉陵江主城段水体藻密度综合影响模型，其中藻密度的单位为104 cell/L，不同参数前的系数反映了该参数与藻密度之间的正负相关性及影响大小。