UGNX11.0有限元分析：振动响应系统运动方程实战

1.单自由度系统运动方程

如图12-1所示的单自由度（SDOF）系统，是一个最简单的动态系统。其中，u（t）代表随时间变化的位移，速度u（t）和加速度u（t）是位移的导出量。

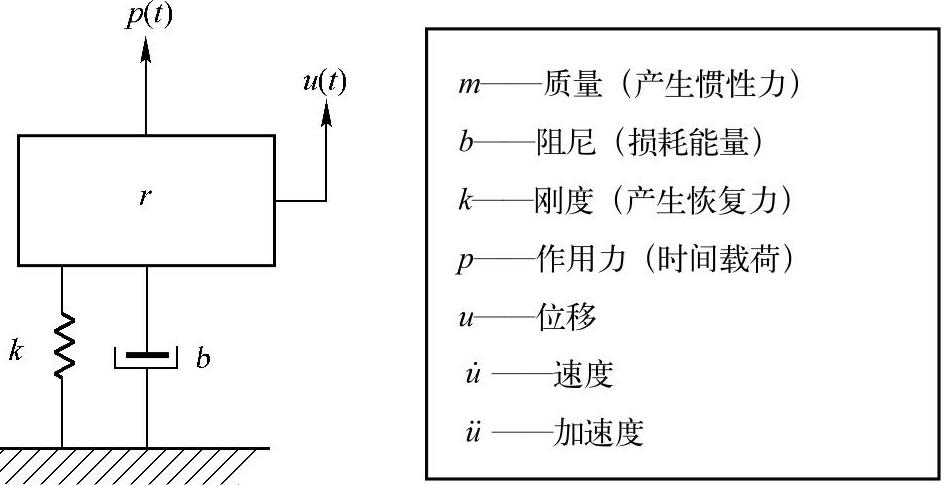
图12-1 单自由度（SDOF）系统

单自由度系统的运动方程为

mu（t）+bu（t）+ku（t）=p（t） （12-1）

这是一个二阶线性微分方程，方程的左边是系统的内力，方程的右边是系统受到的外力。

式中 mu（t） ——惯性力，与质量和加速度成正比；

bu（t） ——粘滞阻尼力，是耗散常数和速度的函数。阻尼力将动能转换为其他形式的能

量（通常是热能），从而衰减振动；

ku（t） ——弹簧力（即恢复力），是刚度和位移的函数；

p（t）——系统受到的外界载荷，它是时间的函数，与结构本身无关。

2.无阻尼自由振动

在式（12-1）中，如果方程的右边为零（没有外界载荷），并忽略阻尼，则方程简化为

mu（t）+ku（t）=0 （12-2）

这是单自由度系统无阻尼自由振动的微分方程，该方程的解为

u（t）=A₁cosω_nt+A₂sinω_nt （12-3）

式中，ω_n是结构的自然圆频率（或固有圆频率），单位是rad/s（国际单位制）。

自然频率（或固有频率）f_n定义如下，单位是Hz（国际单位制）。

在式（12-3）中，A₁、A₂是积分常数，这两个常数取决于系统的初始状态。已知系统的初始位移u（t=0）和初始速度u（t=0），可以求得A₁、A₂。

将t=0代入式（12-3），得到

A₁=u（t=0） （12-6）

对式（12-3）等号两边同时求一阶导数，并将t=0代入，得到

因此，单自由度系统无阻尼自由振动，任意时刻的位移可以表示为

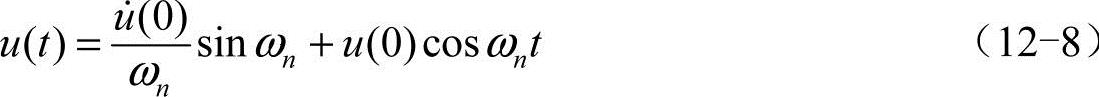
如果引入幅值A和相位φ：

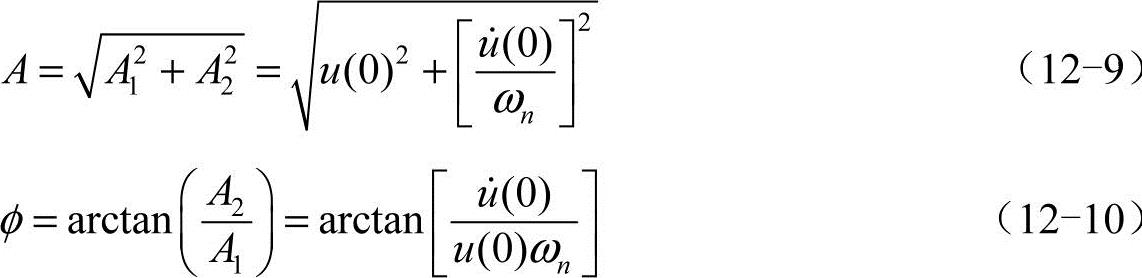
则：A₁=Acosφ，A₂=Asinφ。

式（12-3）又可以写成

u（t）=Acosφcosω_nt+Asinφsinω_nt （12-11）

即

u（t）=Acos（ω_nt-φ） （12-12）

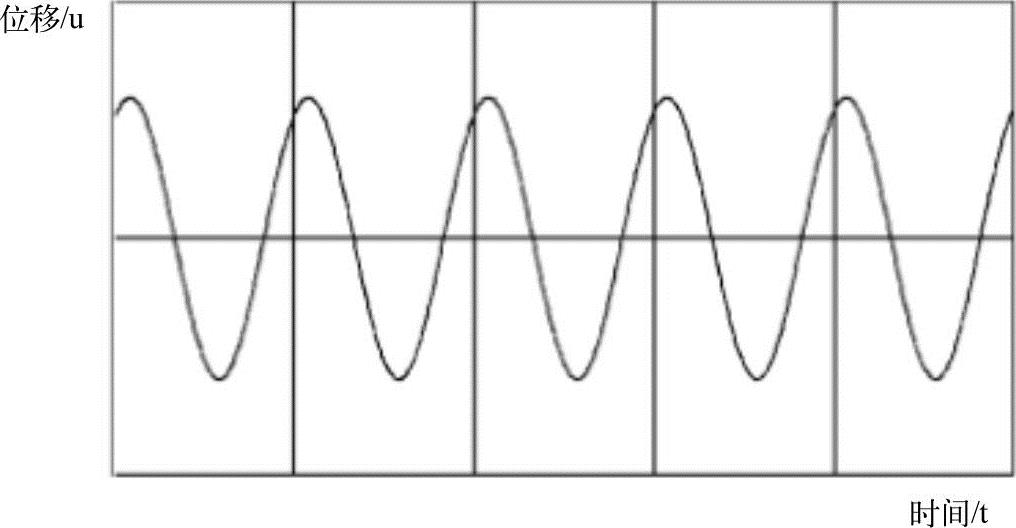
它是初始位移和初始速度的函数，函数曲线如图12-2所示。

(www.xing528.com)

图12-2 无阻尼自由振动

3.粘滞阻尼自由振动

如果考虑阻尼，则需要求解有阻尼的自由振动问题。对于单自由度粘滞阻尼系统，自由振动的运动方程为

mu（t）+bu（t）+ku（t）=0 （12-13）

临界阻尼用b_cr表示，定义为

阻尼比ζ，即b与b_cr的比值：

ζ=b/b_cr （12-15）

根据阻尼比的大小，可以将阻尼分为以下三种情况。

1）ζ=1，临界阻尼情况。

2）ζ>1，过阻尼情况。

3）0<ζ<1，欠阻尼情况。

图12-3显示了各种阻尼情况下的位移响应，其中ζ=0即无阻尼自由振动的情况。

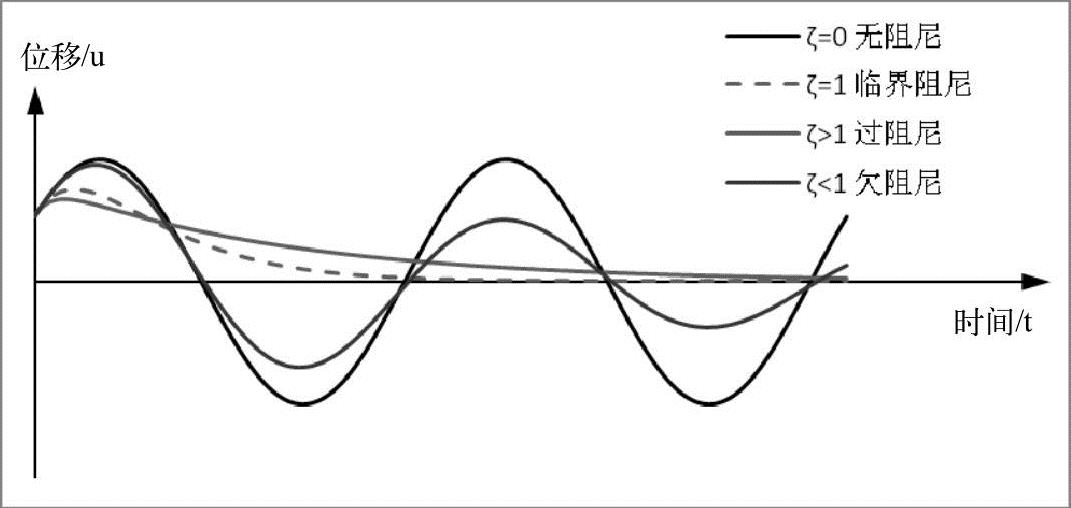
图12-3 各种阻尼情况下的位移响应

工程应用中比较常见的是欠阻尼响应情况。阻尼自然圆频率为ω_d，它与无阻尼的自然圆频率ω_n之间的关系如下

每个振动周期的振幅相对于上一个周期都会衰减，振幅的包络线遵循指数衰减规律，如图12-4所示。

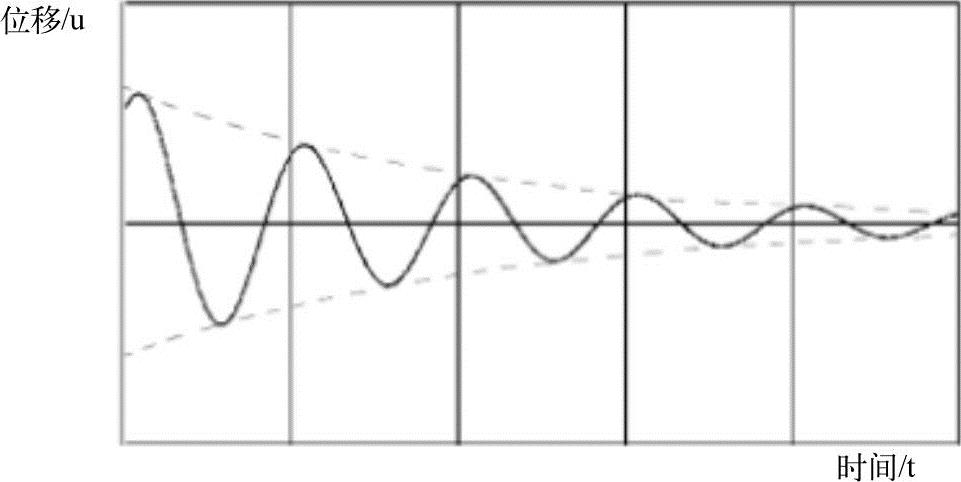
图12-4 欠阻尼自由振动

4.受迫振动

受迫振动分析，用于分析结构在外界激励作用下的动态响应。以简谐力的激励为例，运动方程如下

mu（t）+bu（t）+ku（t）=psinωt （12-17）

方程右边表示圆频率为ω的简谐力，与结构的固有圆频率ω_n无关。如果把这个简谐力的幅值p作为静态载荷施加给结构，则结构的静态位移δ_st=p/k。

无阻尼情况，结构动态位移响应的幅值A与δ_st的比值（即动态放大系数）：

当激励频率接近于结构的固有频率时，ω/ω_n趋近于1，分母趋近于0，这样会导致动态放大系数无穷大。这种情况在物理上表现为动态响应的振幅非常大，即共振现象。

考虑阻尼比ζ，动态放大系数为

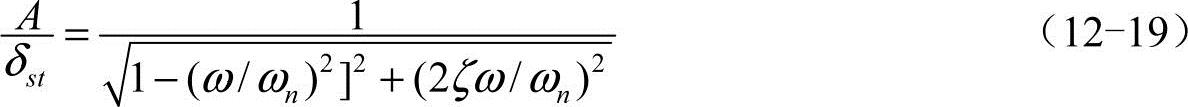
固有频率、激励频率和相位角，三者之间的关系是描述动态响应特征的关键。

● 如果ω/ω_n接近0，则动态放大系数接近1。位移响应的幅值与静态位移接近，相位角与外界激励一致。

● 如果ω/ω_n远大于1，则动态放大系数接近0。位移响应非常小，结构几乎不响应外界激励。因为载荷变化得太快，结构来不及对其进行响应。位移响应的相位角，与外界激励相差180°。即瞬时位移的方向与该时刻力的方向相反。

● 如果ω/ω_n=1，则发生共振，放大系数是1/（2ζ），相位角与外界激励相差270°。

图12-5显示了动态放大系数和相位角关于激励频率的变化规律。

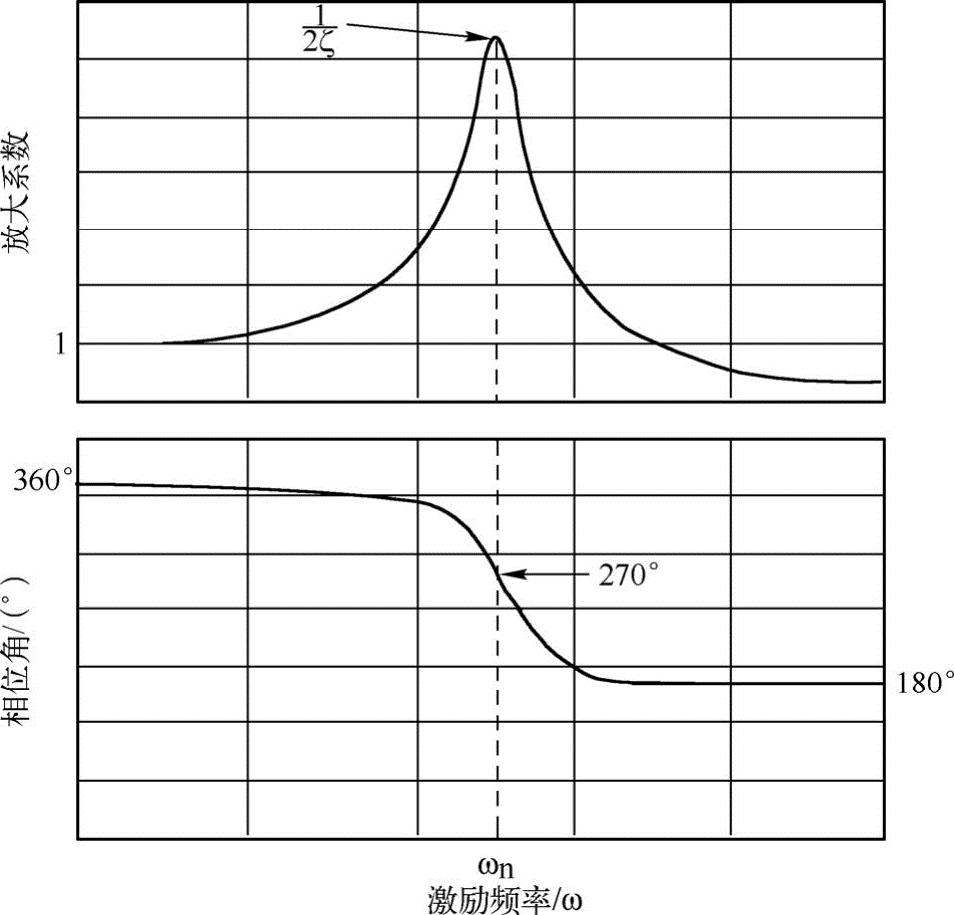
图12-5 简谐力激励的动态响应