【摘要】:双线性弹塑性材料模型,所描述的应力-应变关系如图10-6所示,通过两条直线段来模拟弹塑性材料的本构关系,两条直线的斜率分别为弹性模量E和切线模量Et。NX Nastran中定义的硬化模量H与弹性模量E和切线模量Et之间的关系如下:NX 11.0轴对称单元的有限元分析功能,目前只支持SOL101、SOL106和SOL601三种解算方案。本章中SOL101分别采用3D模型和轴对称单元进行分析,SOL105和SOL106只采用3D模型进行分析,SOL601只采用轴对称单元进行分析。
双线性弹塑性材料模型,所描述的应力-应变关系(本构模型)如图10-6所示,通过两条直线段来模拟弹塑性材料的本构关系,两条直线的斜率分别为弹性模量E和切线模量Et。应力和应变在材料屈服以前,按照弹性模量成比例变化;屈服以后,按比弹性模量小的另一个模量(切线模量)成比例变化。
NX Nastran中定义的硬化模量H与弹性模量E和切线模量Et之间的关系如下:

NX 11.0轴对称单元的有限元分析功能,目前只支持SOL101、SOL106和SOL601三种解算方案。而SOL106中的轴对称单元,只有在超弹性分析中表现出非线性,其他情况下仍然是线性的。SOL601可以完全支持轴对称单元的非线性分析问题。
本章中SOL101分别采用3D模型和轴对称单元进行分析,SOL105和SOL106只采用3D模型进行分析,SOL601只采用轴对称单元进行分析。由于轴对称模型具有无数个对称面(任何一个通过中心对称轴的平面都是对称面),结合上一章介绍的对称问题的有限元分析方法,可以拆分出1/180模型(见图10-7),划分3D六面体单元进行分析。(https://www.xing528.com)
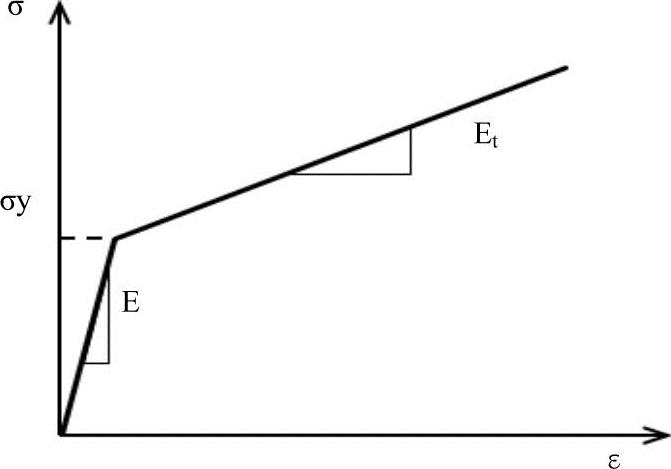
图10-6 双线性弹塑性材料模型
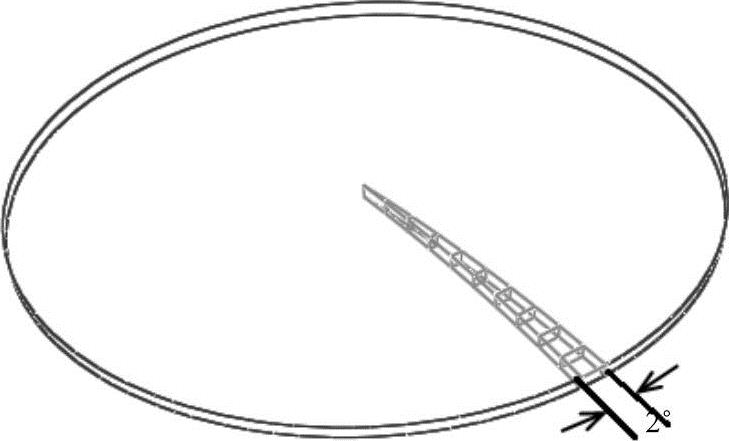
图10-7 1/180模型示意图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




