单因素方差分析教程-高职应用数学　下册

只考虑一个因素A对所关心的指标的影响，A取几个水平，在每个水平上作若干个试验，试验过程中除A外其他影响指标的因素都保持不变（只有随机因素存在），我们的任务是从试验结果推断，因素A对指标有无显著影响，即当A取不同水平时指标有无显著差别.

A取某个水平下的指标视为随机变量，判断A取不同水平时指标有无显著差别，相当于检验若干总体的均值是否相等.

1.数学模型

设A取r个水平A1，A2，…，Ar，在水平Ai下总体xi服从正态分布N（μi，σ2），i=1，…，r这里μi，σ2未知，μi可以互不相同，但假定xi有相同的方差.又设在每个水平Ai下作了ni次独立试验，即从中抽取容量为ni的样本，记作xij，j=1，…，ni，xij服从N（μi，σ2），i=1，…，r，j=1，…，ni且相互独立.将这些数据列成表9-27（单因素试验数据表）的形式.

表9-27 单因素试验数据

单因素方差分析的基本步骤：

（1）将第i行称为第i组数据.判断A的r个水平对指标有无显著影响，提出假设：H0：μ1=μ2=…=μr；H1：μ1，μ2，…，μr不全相等；

（2）计算检验统计量和概率P值；

（3）给定显著水平与P值做比较：如果P值小于显著水平，则应该拒绝原假设，反之就不能拒绝原假设.

2.单因素方差分析SPSS基本步骤

在利用SPSS进行单因素方差分析时，应注意数据的组织形式.SPSS要求定义两个变量分别存放观测变量值和控制变量的水平值.基本操作步骤如下：

（1）选择菜单分析→比较均值→单因素方差分析；

（2）将观测变量选择到因变量列表；

（3）将控制变量选择到因子.控制变量有几个不同的取值表示控制变量有几个水平.

（4）方差齐性检验.由于方差分析的前提是各水平下的总体服从正态分布并且方差相等，因此有必要对方差齐性进行检验，即对控制变量不同水平下各观测变量不同总体方差是否相等进行分析.SPSS单因素方差分析中，方差齐性检验采用了方差同质性（HomogeneityofVariance）的检验方法，其零假设是各水平下观测变量总体方差无显著性差异，实现思路同SPSS两独立样本t检验中的方差齐性检验；

（5）多重比较检验.多重比较检验就是分别对每个水平下的观测变量均值进行逐对比较，判断两均值之间是否存在显著差异.其零假设是相应组的均值之间无显著差异.

上面的基本分析可以判断控制变量是否对观测变量产生了显著影响.如果控制变量确实对观测变量产生了显著影响，进一步还应确定，控制变量的不同水平对观测变量的影响程度如何，其中哪个水平的作用明显大于其他水平，哪些水平的作用是不显著的.例如已经确定不同施肥量会对农作物的产量产生显著影响，便希望进一步了解究竟是10kg、20kg还是30kg施肥量最有利于提高产量，哪种施肥量对农作物产量没有显著影响.掌握了这些信息，我们就能够制定合理的施肥方案.

SPSS提供的多重比较检验的方法比较多，有些方法适用在各总体方差相等的条件下，有些适用在方差不相等的条件下.其中LSD方法适用于各总体方差相等的情况，特点是比较灵敏；Tukey方法和S-N-K方法适用于各水平下观测变量个数相等的情况；Scheffe方法比Tukey方法不灵敏.

至此，SPSS便自动分解观测变量的方差，计算组间方差、组内方差、F统计量以及对应的概率P值，完成单因素方差分析的相关计算，并将结果显示到输出窗口中.

例1 为考察5名工人的劳动生产率是否相同，记录了每人4d的产量，并算出其平均值，见表9-28.你能从这些数据推断出他们的生产率有无显著差别吗？

表9-28 劳动产量数据

解 ①选择菜单分析→比较均值→单因素方差分析；(www.xing528.com)

②将工人的产量选到因变量列表，将工人序号选择到因子.

③方差齐性检验.选择选项里的方差同质性检验.

④多重比较检验.若方差分析有显著差异，根据方差齐性检验选择相对应的方法，见表9-29.

表9-29 方差齐性检验

表9-30 ANOVA

结果表明：由表9-29得，P=0.747＞α=0.05，故接受H0，表明方差齐.由表9-30得，P=0.111＞α=0.05，故接受H0，即5名工人的生产率没有显著差异.

例2 用4种工艺生产灯泡，从各种工艺制成的灯泡中各抽出了若干个测量其寿命，结果见表9-31，试推断这几种工艺制成的灯泡寿命是否有显著差异.

灯泡寿命单因素方差分析

表9-31 灯泡寿命数据

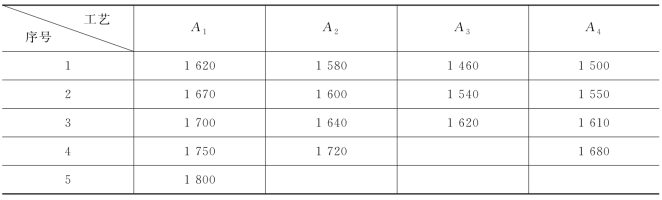
解 解的过程同上.

表9-32 方差齐性检验

表9-33 ANOVA

表9-34 多重比较

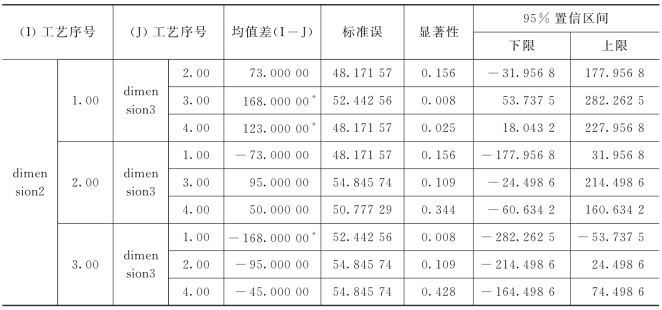
注：*.均值差的显著性水平为0.05.

结果表明：表9-32的方差齐性检验中P值=0.952＞α=0.05，接受原假设表明方差齐，表9-33的单因素方差分析中P值=0.033＜α=0.05，拒绝原假设表明4中工艺存在显著性差异.从表9-34的多重比较可看出，只有工艺1和工艺3，4存在显著性差异，工艺1要显著优于工艺3，4.