用样本来推断总体,需要知道样本统计量的分布,而样本又是一组与总体同分布的随机变量,所以样本统计量的分布依赖于总体的分布.当总体服从一般的分布时,求某个样本统计量的分布是很困难的,只有在总体服从正态分布时,一些重要的样本统计量(均值、标准差)的分布才有便于使用的结果.另一方面,现实生活中需要进行统计推断的总体,多数统计中人们在正态总体的假定下研究统计量的分布,是必要的与合理的.
利用样本对总体进行统计推断的一类问题是参数估计,即假定已知总体的分布,通常是X~N(μ,
σ2),估计有关的参数,如μ,σ2.参数估计分点估计和区间估计两种.点估计是用样本统计量确定总体参数的一个数值.点估计虽然给出了待估参数的一个数值,却没有告诉我们这个估计值的精度和可信程度.区间估计给出总体未知参数所在的可能区间即置信区间,它会随样本的不同而不同,可以解决参数估计的精确度与可靠性问题,它能够以一定的置信度保证估计的正确性.一般情况下,置信度越高,允许误差越大,精确度越低.
SPSS参数估计,选择分析→比较均值,有单个样本T检验,独立样本T检验,配对样本T检验,根据数据选择相应检验.运行检验过程可得到两个总体均值之差在一定把握程度下的区间估计.利用配对样本可使两个样本中许多其他因素保持完全相同.因此估计误差会比独立样本小.
1.若是1个样本则运行单个样本T检验.
2.若是两个独立样本(n1≠n2)则运行两个独立样本之差T验Independent-SamplesT Test过程.
3.若是两个独立样本(n1=n2),则运行两个配对样本均值之差的T检验Paired-Samples T Test过程.
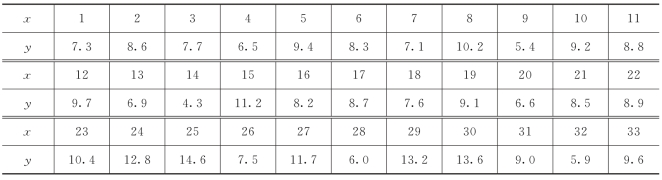
例3 某电视台广告部想要估计一下,各企业在该电台的黄金时间播放电视广告后的一个月内的平均受益量.为此他们抽取了33家播放广告的同类企业的随机样本,资料见表9-16,x表示企业序号,y表示利润增量(万元).
表9-16 平均收益量
解 该电视台宣布的平均收益量应该是最小收益量,故构造95%置信下限.
(1)把利润增量(万元)输入到SPSS数据视图;
(2)选择分析→比较均值→单个样本T检验;
(3)把利润增量(万元)选入检验变量中;
(4)单击确定按钮执行.所得结果见表9-17和表9-18.
表9-17 单个样本统计量

表9-18 单个样本检验
 (https://www.xing528.com)
(https://www.xing528.com)
结果表明:表9-17所示33家平均受益量为8.864万元,标准差为2.4027万元.表9-18所示该项电视台可以95%的置信度宣布在该电台黄金时间做广告给企业带来的平均受益量至少在8.012万元以上.
例4 某一个新的制造过程可以增加电池的使用寿命,假设电池使用寿命服从正态分布.在新电池中随机抽取15个,而在旧电中随机抽取12个同时测试其使用寿命,资料如下:新电池(日):18.2/10.4/12.6/18.0/11.7/15.0/24.0/17.6/23.6/24.8/19.3/20.5/19.8/17.1/16.3.
旧电池(日):12.1/17.5/8.6/13.9/7.8/15.1/17.9/10.6/13.8/14.2/15.3/11.6.
求新、旧两种电池平均使用寿命之差95%的置信区间.
解 (1)定义变量x和g,输入数据资料,新旧电池寿命数据全部输入x同一列中,g分别取1和2,新电池组号为1,旧电池组号为2;
(2)由于是样本量不相等的两组数据,所以选择分析→比较均值→独立样本T检验;
(3)将变量x放入检验变量栏中;

电池寿命参数估计
(4)激活DefineGroups 按钮,打开该对话框Groups1中输入1Groups2中输入2,单击Continue返回主对话框;
(5)单击OK按钮执行,所得结果见表9-19和表9-20.
表9-19 组统计量

表9-20 独立样本检验

结果表明:表9-19得出新电池和旧电池寿命的均值,标准差.新电池的平均使用寿命明显长于旧电池.表9-20得出新旧电池平均使用寿命之差的95%的置信区间为:若两个样本方差相等则为(1.6352,7.8180);若两个样本方差不等则为(1.7402,7.7130).
注意 方差齐性检验,即要求所有处理随机误差的方差都要相等,换句话说不同处理不能影响随机误差的方差.由于随机误差的期望一定为0,这实际是要求随机误差有共同的分布.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




