高职应用数学下册-统计基本概念

1.总体和样本

总体是人们研究对象的全体，又称母体，如工厂一天生产的全部产品（按合格品及废品分类），学校全体学生的身高总体中的每一个基本单位称为个体，个体的特征用一个变量（如x）来表示，如一件产品是合格品记x=0，是废品记x=1；一个身高170cm的学生记x=170cm.

从总体中随机产生的若干个个体的集合称为样本，或子样，如n件产品，100名学生的身高，或者一根轴直径的10次测量.实际上这就是从总体中随机取得的一批数据，不妨记作x1，x2，…，xn，n称为样本容量.简单地说，统计的任务是由样本推断总体.

2.频数表和直方图

一组数据（样本）往往是杂乱无章的，做出它的频数表和直方图，可以看作是对这组数据的一个初步整理和直观描述.

将数据的取值范围划分为若干个区间，然后统计这组数据在每个区间中出现的次数，称为频数，由此得到一个频数表.以数据的取值为横坐标，频数为纵坐标，画出一个阶梯形的图，称为直方图，或频数分布图.

若样本容量不大，能够手工做出频数表和直方图，当样本容量较大时则可以借助SPSS这样的软件了.让我们以下面的例子为例，介绍频数表和直方图的作法.

例1 某车间30名工人按每天加工某种零件数见表9-12.请对加工零件数进行频数分析.

频数分析

表9-12 某车间工人每天加工某种零件件数

解 （1）定义工人编号和加工零件数的变量名分布为NO和X，然后输入变量NO和X的原始数据.

（2）SPSS在未特别指定的情形下，直方图或频数分布表是按照原始数值逐一作频数分布的，这与日常需要的等距分组、且组数保持在一定数目的要求不符.因此，在调用频数统计过程命令之前，可先对原始数据进行预处理：已知最小值为84，最大值为128，故可要求分成5组，起点为80，组距为10，根据SPSS转换中重新编码为不同变量进行分组，定义变量名为X2，第一组为80～90，第二组为90～100，第三组为100～110，第四组为110～120，第五组为120～130.

（3）选择分析→描述统计→频率，弹出频率主对话框.现欲对X2进行频数分析，在对话框左侧的变量列表中选X2，勾选左下方的显示频率表格，单击图标按钮，选择条形图.单击继续，选择确定.

图9-1 加工零件数直方图

表9-13 加工零件数频率

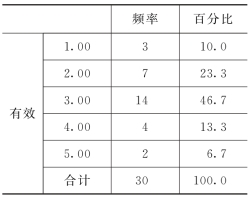
表9-13给出看了每组的频率和百分比，第三组的频率和百分比最高，其次是第二组.从直方图9-1上可以看出，加工零件数大致呈中间高、两端低的钟形；要想从数值上给出更确切的描述，需要进一步研究反映数据特征的所谓“统计量”.直方图所展示的加工零件数的分布形状可看作正态分布，当然也可以用这组数据对分布作假设检验.

3.统计量

假设有一个容量为n的样本（即一组数据），记作x=（x1，x2，…，xn），需要对它进行一定的加工，才能提出有用的信息，用作对总体（分布）参数的估计和检验.统计量就是加工出来的、反映样本数量特征的函数，它不含任何未知量.

下面我们介绍几种常用的统计量.

（1）表示位置的统计量——算术平均值和中位数.

算术平均值（简称均值）描述数据取值的平均位置，记作，

中位数是将数据由小到大排序后位于中间位置的那个数值.

（2）表示变异程度的统计量——标准差、方差和极差.

标准差s定义为

标准差是各个数据与均值偏离程度的度量，这种偏离不妨称为变异.

方差是标准差的平方s2.

极差是的最大值与最小值之差.

（3）表示分布形状的统计量——中心矩、偏度和峰度.

随机变量x的r阶中心矩为E（x-Ex）r.随机变量x的偏度和峰度指的是x的标准化变量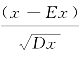的三阶中心矩和四阶中心矩：

偏度反映分布的对称性，v1＞0称为右偏态，此时数据位于均值右边的比位于左边的多；v1＜0称为左偏态，情况相反；而v1接近0则可认为分布是对称的.(www.xing528.com)

峰度是分布形状的另一种度量，正态分布的峰度为3，若v2比3大得多，表示分布有沉重的尾巴，说明样本中含有较多远离均值的数据，因而峰度可以用作衡量偏离正态分布的尺度之一.

例2 学生的身高和体重.

学校随机抽取100名学生，测量他们的身高cm和体重kg，所得数据见表9-14，用SPSS计算这些数据的统计量.

表9-14 身高体重数据

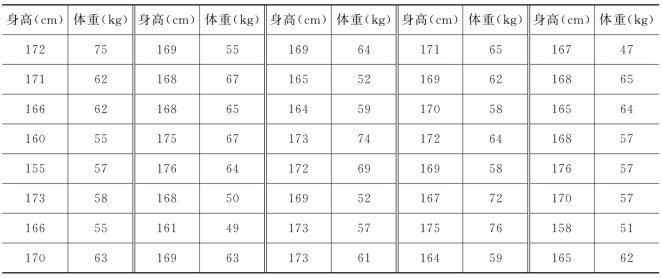
（续表）

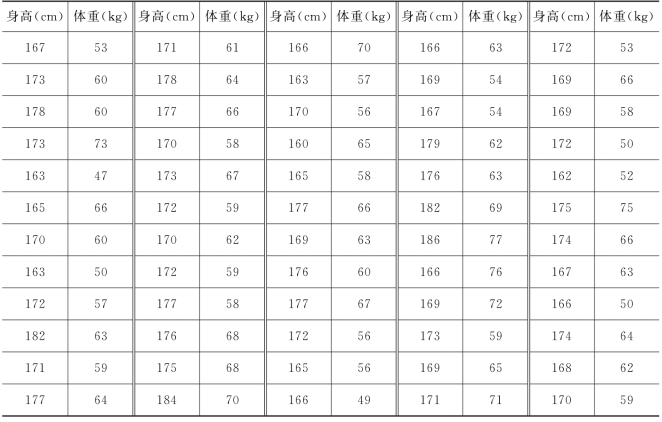
解 把数据输入到SPSS中，选择分析→描述统计→频率，把身高cm和体重kg选入变量中，单击统计量，选择均值，中位数，标准差，方差，范围（极差），偏度，峰度计算出数据的统计量，所得结果见表9-15.

表9-15 统计量

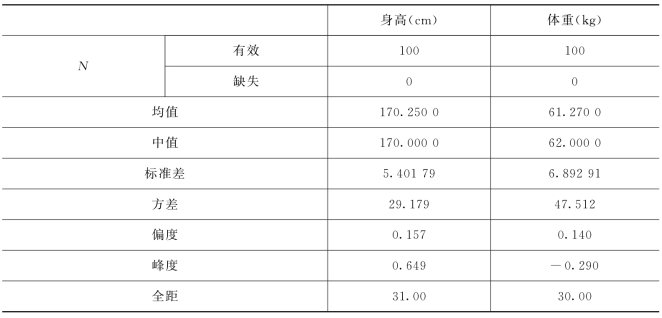
统计量中最重要、最常用的是均值和标准差，由于样本是随机变量，它们作为样本的函数自然也是随机变量，当用它们去推断总体时，有多大的可靠性就与统计量的概率分布有关，因此我们需要知道几个重要分布的简单性质.

4.统计中几个重要的概率分布

（1）分布函数、密度函数.

随机变量的特性完全由它的（概率）分布函数或（概率）密度函数来描述.设有随机变量X，其分布函数定义为X≤x 的概率，即F（x）=P{X≤x}.若X是连续型随机变量，则其密度函数p（x）与F（x）的关系为

上a分位数是下面常用的一个概念，其定义为：对于0＜a＜1，使某分布函数F（x）=1-a的x，称为这个分布的上a分位数，记作xa.

前面画过的直方图是频数分布图，频数除以样本容量n，称为频率，n充分大时频率是概率的近似，因此直方图可以看作密度函数图形的（离散化）近似.

（2）统计中几个重要的概率

①正态分布

正态分布随机变量X 的密度函数曲线呈中间高两边低、对称的钟形，期望（均值）EX=μ，方差DX=σ2，记作X～N（μ，σ），σ称均方差或标准差，当μ=0，σ=1时称为标准正态分布，记作X～N（0，1）.正态分布完全由均值μ和方差σ2决定，它的偏度为0，峰度为3.

正态分布可以说是最常见的（连续型）概率分布，成批生产时零件的尺寸，射击中弹着点的位置，仪器反复量测的结果，自然界中一种生物的数量特征等，多数情况下都服从正态分布，这不仅是观察和经验的总结，而且有着深刻的理论依据，即在大量相互独立的、作用差不多大的随机因素影响下形成的随机变量，其极限分布为正态分布.

鉴于正态分布的随机变量在实际生活中如此地常见，记住下面3个数字是有用的：

68%的数值落在距均值左右1个标准差的范围内，即

P｛μ-σ≤X≤μ+σ｝=0.68;

95%的数值落在距均值左右2个标准差的范围内，即

P｛μ-σ≤X≤μ+σ｝=0.95;

99.7%的数值落在距均值左右3个标准差的范围内，即

P｛μ-σ≤X≤μ+σ｝=0.997.

②χ2分布

若X1，X2，…，Xn为相互独立的，服从标准正态分布N（0，1）的随机变量，则它们的平方和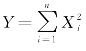服从χ2分布，记作Y～χ2（n），n称自由度，它的期望EY=n，方差DY=2n.

③t分布

若Y～χ2（n），且相互独立，则服从t分布，记作T～t（n），n称自由度.

t分布又称学生氏（Student）分布.

t分布的密度函数曲线和N（0，1）曲线形状相似.理论上n→∞时，T～t（n）→N（0，1），实际上当n＞30时他与N（0，1）就相差无几了.

④F分布

若X～χ2（n），Y～χ2（n），且互相独立，则服从F分布，记作F～F（n1，n2），（n1，n2）为自由度.