9.1.5.1 随机变量及其分类
在前面的章节里，我们研究了随机事件及其概率，细心的同学可能会注意到在某些例子中，随机事件与实数之间存在某种客观的联系.例如袋中有五个球（三白两黑）从中任取三球，则取到的黑球数可能为0，1，2本身就是数量且随着随机试验结果的变化而变化的，通常称这种量为随机变量.
定义1
若随机试验E的结果可以用一个变量来表示，则称这个变量为随机变量，通常用X表示.
例1 一射手对一射击目标连续射击，则他命中目标的次数.
解 命中目标的次数X为随机变量，X的可能取值为0，1，2，….
例2 某一公交车站每隔5min有一辆汽车停靠，一位乘客不知道汽车到达的时间，则候车时间.
解 候车时间为随机变量X，X的可能取值为[0，5].
从随机变量的取值情况来看，若随机变量的可能取值只要有限个或可列个则该随机变量为离散型随机变量，不是离散型随机变量统称为非离散型随机变量，若随机变量的取值是连续的，称为连续型随机变量，它是非离散型随机变量的特殊情形，本章我们主要研究离散型随机变量.
9.1.5.2 离散型随机变量的概率分布
定义2
设离散型随机变量X的所有可能取值为xi（i=1，2，…），称P{X=xi}=pi，i=1，2，3，…，n为X的概率分布或分布律.
常用见表9-3的表格形式来表示X的概率分布.
表9-3 离散型随机变量的概率分布
由概率的基本性质可知，离散型随机变量的概率分布列具有下面两个性质：
(1)pi≥0,i=1,2,…;
(2)
.
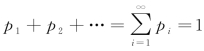例3 设10张CD中有8张是中文版，2张是英文版，从中任取3张，求（1）取得的CD中英文版数目的概率分布；（2）取得的CD中英文版张数不多于1张的概率.
解 （1）设X={取得的CD中英文版的数目}，则X=0，1，2；
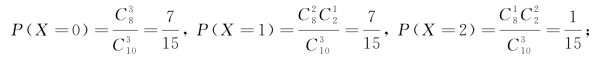
即表9-4.
表9-4 英文版数目的概率分布
(2)
.
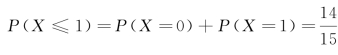要描述一个随机变量时，不仅要说明它能够取哪些值，而且还要指出它取这些值的概率.
只有这样，才能真正完整地刻画一个随机变量，为此，我们引入随机变量的分布函数的概念.
9.1.5.3 离散型随机变量的分布函数
定义3
设X是一个随机变量，称F（x）=P（X≤x）（-∞＜x＜+∞）为X的分布函数.有时记作X～F（x）或FX（x）.设离散型随机变量X的概率分布见表9-5.
表9-5 离散型随机变量X的概率分布
则X的分布函数为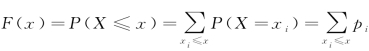
.
例4 设离散型随机变量的分布为见表9-6.
表9-6 离散型随机变量的分布
求F（x）.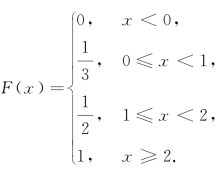
(www.xing528.com)
解 随机变量X的分布函数为：
例5 设随机变量X的分布函数为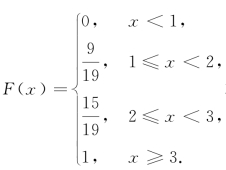
求X的概率分布.
解 随机变量X的概率分布见表9-7.
表9-7 随机变量X的概率分布
9.1.5.4 常见的离散型随机变量概率分布类型
1.两点分布
定义4
若随机变量X的概率分布见表9-8的形式.其中，0＜p＜1，则称X服从两点分布或0～1分布，记作X～（0，1）.
表9-8 随机变量X的0～1分布
两点分布在实际问题中经常遇到，是最基本的分布类型之一，任何随机试验仅有两个可能的结果时，就可以确定一个服从两点分布的随机变量，例如投掷一枚硬币，就是一个常见的两点分布.
2.二项分布
定义5
若随机变量X的分布为：
，k=0，1，2，…，n其中n，p是参数，且0＜p＜1，则称X服从参数为n，p的二项分布，记作X～B（n，p）.见表9-9.
表9-9 随机变量X的二项分布
二项分布的背景是重复独立实验，设在一次试验中，事件A发生的概率为P，则事件A不发生的概率为1～P，那么，在n次试验中，事件A恰好发生k次的概率服从二项分布，特别地，当实验次数n=1时，二项分布就是两点分布.
例6 商场销售的某种商品，其次品率为0.01，假设各件商品之间是否为次品相互独立，这家商场讲每十件商品装成一箱，并保证若发现某箱内多于一个次品，则可退货，求卖出的各箱商品中，被退回的概率.
解 设X={某箱商品的次品数}，则X～B（10，0.01），这箱商品被退回的概率为：
.
课后提升
概率论的起源、发展和应用
1.一批零件中有9个正品和3个次品，安装机器时，从这批零件中任取一个，取到后不放会，直到取得正品为止，求在取得正品前已经取出的次品数X的概率分布.
2.已知随机变量X的概率分布见表9-10.
表9-10 随机变量X的概率分布
求：（1）分布函数
.
3.一栋大厦装有5个同型号的水表，调查表明在任意一个时间段内，每个设备被使用的概率均为0.1，求在同一时刻至少有2个设备被使用的概率.
答案
1.随机变量X的概率分布表见表9-11
表9-11 随机变量X的概率分布
2.(1)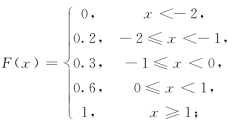
(2)0.8.
3.1-(0.9)5.
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
