高职应用数学下册：独立性与贝努里概型

9.1.4.1 独立性概念

1.两个事件的独立性

定义1

设A，B为两个事件，若P（AB）=P（A）P（B）则称事件A，B是相互独立的，简称为独立的.

例1 一个家庭中有男孩，又有女孩，假定生男孩和生女孩是等可能的，令A={一个家庭中有男孩，又有女孩}，B={一个家庭中最多有一个女孩}对下述两种情形，讨论A，B的独立性.

（1）家庭中有两个小孩；（2）家庭中有三个小孩.

解 （1）有两个小孩的家庭，这时样本空间为：

Ω={（男、男），（男、女），（女、男），（女、女）}，

A={（男、女），（女、男）}，

A={（男、男），（男、女），（女、男）}AB={（男、女），（女、男）}，

于是.

由此可知P（AB）≠P（A）P（B），

所以A，B不独立.

（2）有三个小孩的家庭，样本空间Ω={（男、男、男），（男、男、女），（男、女、男），（女、男、男）（男、女、女），（女、女、男），（女、男、女），（女、女、女）}.

由等可能性可知，这8个基本事件的概率都是，这时A包含了6个基本事件，B包含了4个基本事件，AB包含了3个基本事件

显然P（AB）=P（A）P（B），从而A与B相互独立.

2.多个事件的独立性

定义2

设三个事件A，B，C满足

P(AB)=P(A)P(B),

P(AC)=P(A)P(C),

P(CB)=P(C)P(B),

称A，B，C两两相互独立.

定义3

设三个事件A，B，C满足

P(AB)=P(A)P(B),

P(AC)=P(A)P(C),

P(CB)=P(C)P(B),

且P（ABC）=P（A）P（B）P（C）称A，B，C相互独立.

由三个事件的独立性可知，若A，B，C两两相互独立，不能得出A，B，C一定相互独立，反之也不成立.

例2 一个均匀的正四面体，其第一面染成红色，第二面染成白色，第三面染成黑色第四面上同时染上红、黑、白三色，以A，B，C分别记投一次四面体，出现红、白、黑颜色的事件，则.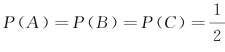

解 ，，

故A，B，C两两相互独立，

但不能推出P（ABC）=P（A）P（B）P（C），故A，B，C不是相互独立的.

3.独立性的性质

性质1 四对事件中有一对相互独立，则其他三对也相互独立.

性质2 设A1，A2，…，An相互独立，则将其中任意m个（1≤m≤n）换成其对立事件，则所得n个事件也相互独立.特别地，若A1，A2，…，An相互独立，则也相互独立.

例3 假若每个人血清中含有肝炎病的概率为0.4%，混合100个人的血清，求此血清中含有肝炎病毒的概率？

解 设Ai={第I个人血清中含有肝炎病毒} i=1，2，…，100

可以认为A1，A2，…，A100相互独立，所求的概率为(www.xing528.com)

虽然每个人有病毒的概率都是很小，但是混合后，则有很大的概率，在实际工作中，这类效应值得充分重视.

4.独立与互斥之间的关系

互斥和独立是两个完全不同的概念；

A，B相互独立不能推出A，B互斥，反之也不成立.

9.1.4.2 贝努里概型

1.试验的独立性

如果两次试验的结果是相互独立的，称两次试验是相互独立的.当然，两次试验是相互独立的，由此产生的事件也是相互独立.

若试验只有两个可能的结果：A及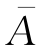，称这个试验为贝努里试验.

2.贝努里概型

设随机试验具有如下特征：

（1）每次试验是相互独立的；

（2）每次试验有且仅有两种结果：事件A和事件；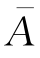

（3）每次试验的结果发生的概率相同即.

称试验E表示的数学模型为贝努里概型.若将试验做了n次，则这个试验也称为n重贝努里试验.

由此可知“一次抛掷n枚相同的硬币”的试验可以看作是一个n重贝努里试验.

一个贝努里试验的结果可以记作

ω=(ω1,ω2,…,ωn).

其中ωi（1≤i≤n）或者为A或者为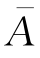，因而这样的ω共有2n个，它们的全体就是贝努里试验的样本空间Ω.

ω=(ω1,ω2,…,ωn)∈Ω.

如果ωi（1≤i≤n）中有k个A，则必有n-k个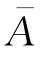.于是由独立性即得P（ω）=pkqn-k.

如果要求“n重贝努里试验中事件A出现k次”这一事件的概率

记Bk={n重贝努里试验中事件A出现k次}.

由概率的可加性k=0，1，2，…，n

在n次贝努里试验.事件A至少发生一次的概率为1-qn.

例4 金工车间有10台同类型的机床，每台机床配备的电功率为10kW，已知每台机床工作时，平均每小时实际开动12min，且开动与否是相互独立的.现因当地电力供紧张，供电部门只提供50kW的电力给这10台机床.问这10台机床能够正常工作的概率为多大？

解 50kW电力可用时供给5台机床开动，因而10台机床中同时开动的台数为不超过5台时都可以正常工作，而每台机床只有“开动”与“不开动”的两种情况，且开动的概率为.不开动的概率为.设10台机床中正在开动着的机床台数为ξ，则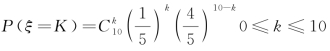于是同时开动着的机床台数不超过5台的概率为

由此可知，这10台机床能正常工作的概率为0.994，也就是说这10台机床的工作基本上不受电力供应紧张的影响.

例5 某人有一串m把外形相同的钥匙其中只有一把能打开家门.有一天该人酒醉后回家，下意识地每次从m把钥匙中随便拿一把去开门，问该人第k次才把门打开的概率为多少？

解 因为该人每次从m把钥匙中任取一把（试用后不做记号又放回）所以能打开门的一把钥匙在每次试用中恰被选种的概率为，易知，这是一个贝努里试验，在第k次才把门打开，意味着前面k-1次都没有打开，于是由独立性即得

例6 （巴拿赫火柴问题）某数学家常带有两盒火柴（左、右袋中各放一盒）每次使用时，他在两盒中任抓一盒，问他首次发现一盒空时另一盒有r根的概率是多少？（r=0，1，2，…，N，N为最初盒子中的火柴数）

解 设选取左边衣袋为“成功”，于是相继选取衣袋，就构成了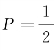的贝努里试验.当某一时刻为先发现左袋中没有火柴而右袋中恰有r根火柴的事件相当于恰有N-r次失败发生在第2N-r根火柴，其中从左袋中取了N根，并且在2N-r+1次取火柴还要从左袋中取，才能发现左袋已经取完，因此

由对称性可知，首次发现右袋中没有火柴而左袋中恰有r根的概率为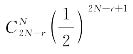故所求的概率为.

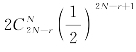课后提升

1.三人独立的想同一飞盘射击，他们各自的命中率分别为0.36，0.45，0.65，求分盘被击中的概率.

2.某人投篮的成功率是0.7，连续投5次，求至少有一次成功的概率.

答案

1.0.8768.

2.0.9919.