高职应用数学下册：条件概率与全概率公式

9.1.3.1 条件概率

前面讨论了事件和概率这两个概念，对于给定的一个随机试验，要求出一个指定的随机事件A 的概率P（A），需要花很大的力气，现在将讨论继续引入深入，设两个事件A，B，则有公式P（A∪B）=P（A）+P（B）-P（AB）.

特别地，当A，B为互不相容的两个事件时，有P（A∪B）=P（A）+P（B）此时有P（A）及P（B）即可求得P（A∪B），但在一般情形下，为求得P（A∪B）还应该知道P（AB）.因而很自然要问，能不能通过P（A）及P（B）求得P（AB），先看一个简单的例子.

例1 考虑有两个孩子的家庭，假定男女出生率一样，则两个孩子（依大小排列）的性别分别为（男，男），（男，女），（女，男），（女，女）的可能性是一样的.

解 若记A={“随机抽取一个这样的家庭中有一男一女”}.

则但如果我们事先知道这个家庭至少有一个女孩，则上述事件的概率为.

这两种情况下算出的概率不同，这也很容易理解，因为在第二种情况下我们多知道了一个条件.记B={“这个家庭中至少有一个女孩”}，因此我们算得的概率是“在已知事件B发生的条件下，事件A发生”的概率，这个概率称为条件概率，记为P（A|B）.

这虽然是一个特殊的例子，但是容易验证对一般的古典概型，只要P（B）＞0上述等式总是成立的，同样对几何概率上述关系式也成立.

9.1.3.2 乘法公式

由条件概率的定义可知，当P（A）＞0时，

P(AB)=P(A)P(B|A).

同理当P（B）＞0时，P（AB）=P（B）P（A|B），

这个公式称为乘法公式

乘法公式可以推广到n个事件的情形，

P(A1A1…An)=P(A1)P(A2|A1)P(A3|A1A2)…P(An|A1A2…An-1)(P(An|A1A2…An-1)＞0).

例2 甲、乙两市都位于长江下游，据一百多年来的气象记录，知道在一年中的雨天的比例甲市占20%，乙市占18%，两地同时下雨占12%.

记A={甲市出现雨天} B{乙市出现雨天}

求：（1）两市至少有一市是雨天的概率；

（2）乙市出现雨天的条件下，甲市也出现雨天的概率；

（3）甲市出现雨天的条件下，乙市也出现雨天的概率.

解 （1）两市至少有一市是雨天的概率为：

P(A∪B)=0.26;

（2）乙市出现雨天的条件下，甲市也出现雨天的概率为：

P(A|B)=0.67;

（3）甲市出现雨天的条件下，乙市也出现雨天的概率为：(www.xing528.com)

P(B|A)=0.60.

例3 （抽签问题）有一张电影票，7个人抓阄决定谁得到它，问第i个人抓到票的概率是多少（i=1，2，…，7）？

解 设Ai=“第i个人抓到票” （i=1，2，…，7）

显然.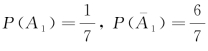

如果第二个人抓到票的话，必须第一个人没有抓到票.

这就是说，所以.

于是可以利用概率的乘法公式，因为在第一个人没有抓到票的情况下，第二个人有希望在剩下的6个阄中抓到电影票，

所以，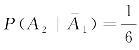

类似可得：

9.1.3.3 全概率公式

为了求得比较复杂事件的概率，我们往往需要先把一个事件分解为两个（或若干个）互不相容的较简单的事件的并，求出这些较简单事件的概率，再利用加法公式，便可以求得复杂事件的概率，将这种方法一般化便得到下述定理：

定理1 设B1，B2，…，Bn.是一列互不相容的事件，且有对任何事件A，有.

证明 略.

例4 某工厂有四条生产线生产同一种产品，该四条流水线的产量分别占总产量的15%，20%，30%，35%，又这四条流水线的不合格品率分别为5%，4%，3%，及2%，现在从出厂的产品中任取一件，问恰好抽到不合格品的概率为多少？

解 A={抽到的是不合格品}，B={抽到的是i号生产线的产品}，i=1，2，3，4，显然P（B1）=0.15，P（B2）=0.2，P（B3）=0.3，P（B4）=0.35；

P(A|B1)=0.05,P(A|B2)=0.04,P(A|B3)=0.03,P(A|B4)=0.02;

所以根据全概率公式：

即：恰好抽到不合格品的概率为0.0315.

课后提升

1.从衣服扑克的52张牌中，每一次无放回的抽取1张，一共抽3次，求下列两个事件的概率：（1）3张全是红桃；（2）第三次才抽到红桃.

2.某电器商场销售甲、乙、丙三种电器，已知甲、乙、丙这三种电器的数量各占总量的70%，20%，10%，它们的次品率分别为0.02，0.03，0.04，求任取一台电器它是正品的概率.

答案

1.(1)0.0129;(2)0.1453.

2.0.6.