随机事件与样本空间在《高职应用数学下册》中的探究

9.1.1.1 必然现象与随机现象

在自然界和人的实践活动中经常遇到各种各样的现象，这些现象大体可分为两类：一类是确定的，例如“在一个标准大气压下，纯水加热到100℃时必然沸腾”.“向上抛一块石头必然下落”，“同性电荷相斥，异性电荷相吸”等等，这种在一定条件下有确定结果的现象称为必然现象（确定性现象）；另一类现象是随机的，例如：在相同的条件下，向上抛一枚质地均匀的硬币，其结果可能是正面朝上，也可能是反面朝上，不论如何控制抛掷条件，在每次抛掷之前无法肯定抛掷的结果是什么，这个试验多于一种可能结果，但是在试验之前不能肯定试验会出现哪一种结果.同样地同一门大炮对同一目标进行多次射击（同一型号的炮弹），各次弹着点可能不尽相同，并且每次射击之前无法肯定弹着点的确切位置，以上所举的现象都具有随机性，即在一定条件下进行试验或观察会出现不同的结果（也就是说，多于一种可能的试验结果），而且在每次试验之前都无法预言会出现哪一种结果（不能肯定试验会出现哪一个结果），这种现象称为随机现象.

9.1.1.2 随机试验

我们来看两个试验：

试验1 一盒中有2个完全相同的白球，搅匀后从中摸出一球；

试验2 一盒中有2个相同的球，其中1个白球，1个黑球，搅匀后从中任意摸取一球.

对于试验1而言，在球没有取出之前，我们就能确定取出的球必是白球，也就是说在试验之前就能判定它只有一个确定的结果这种现象就是必然现象（必然现象）.

对于试验2来说，在球没有取出之前，不能确定试验的结果（取出的球）是白球还是黑球，也就是说一次试验的结果（取出的球）出现白球还是黑球，在试验之前无法肯定.

试验2所代表的类型，它有多于一种可能的结果，但在试验之前不能确定试验会出现哪一种结果，这类试验所代表的现象成为随机现象.下面我们给出随机试验的定义.

定义1

一个试验如果满足下述条件：

（1）试验可以在相同的条件下重复进行；

（2）试验的所有可能结果是明确的，可知道的（在试验之前就可以知道的）并且不止一个；

（3）每次试验总是恰好出现这些可能结果中的一个，但在一次试验之前却不能肯定这次试验出现哪一个结果.

称这样的试验是一个随机试验，为方便起见，也简称为试验，今后讨论的试验都是指随机试验.

9.1.1.3 基本事件与样本空间

对于随机试验来说，我们感兴趣的往往是随机试验的所有可能结果.例如掷一枚硬币，我们关心的是出现正面还是出现反面这两个可能结果.若我们观察的是掷两枚硬币的试验，则可能出现的结果有（正、正），（正、反），（反、正），（反、反）四种，如果掷三枚硬币，其结果还要复杂，但还是可以将它们描述出来的，总之为了研究随机试验，必须知道随机试验的所有可能结果.

1.基本事件

通常，据我们研究的目的，将随机试验的每一个可能的结果，称为基本事件.因为随机事件的所有可能结果是明确的，从而所有的基本事件也是明确的，例如：在抛掷硬币的试验中“出现反面”，“出现正面”是两个基本事件，又如在掷骰子试验中“出现一点”，“出现两点”，“出现三点”，……，“出现六点”这些都是基本事件.

2.样本空间

基本事件的全体，称为样本空间.也就是试验所有可能结果的全体是样本空间，样本空间通常用大写的希腊字母Ω表示，Ω中的点即是基本事件，也称为样本点，常用ω表示，有时也用A，B，C等表示.

在具体问题中，给定样本空间是研究随机现象的第一步.

例1 一盒中有十个完全相同的球，分别有号码1，2，3，…，10，从中任取一球，观察其标号.

解 令i={取得球的标号为i}，i=1，2，3，…，10则，Ω={1，2，3，4，5，6，7，8，9，10}，ωi={标号为i}，i=1，2，3，…，10，ω1，ω2，ω3，…，ω10为基本事件（样本点）

例2 掷骰子这个随机试验，求样本空间.

解 若考虑出现的点数，则样本空间Ω={1，2，3，4，5，6}；若考虑的是出现奇数点还是出现偶数点，则样本空间Ω={奇数，偶数}.

由此说明，同一个随机试验可以有不同的样本空间.在实际问题中，选择恰当的样本空间来研究随机现象是概率中值得研究的问题.

9.1.1.4 随机事件

我们将样本空间Ω的子集称为随机事件或简称为事件.习惯上用大写英文字母A，B，C 等表示.

比如在例2中样本空间Ω={1，2，3，4，5，6}，我们取子集合A={2，4，6}其对应的事件我们可以理解为投出的点数为偶数，当我们投掷一枚骰子后出现了2点时，我们称事件A发生，当我们投掷一枚骰子后出现了3点时，我们称事件A没有发生.

由于Ω是所有基本事件所组成，因而在一次试验中，必然要出现Ω中的某一基本事件，也就是在试验中Ω必然要发生，所以今后用Ω表示一个必然事件.

相应地，在任意一次试验中不会出现某一个基本事件出现在空集中，也就是说∅永远不可能发生，所以我们用空集∅表示不可能事件.

实质上必然事件就是在每次试验中都发生的事件，不可能事件就是在每次试验中都不发生的事件，必然事件与不可能事件的发生与否，已经失去了“不确定性”即随机性，因而本质上不是随机事件，但为了讨论问题的方便，还是将它看作随机事件.

9.1.1.5 事件的关系与运算

对于随机试验而言，它的样本空间Ω可以包含很多随机事件，我们需要研究随机事件的规律，通过对较简单事件规律的研究在掌握更复杂事件的规律，为此需要研究事件之间和事件之间的关系与运算.

若没有特殊说明，认为样本空间Ω是给定的，且还定义了Ω中的一些事件，A，B，Ai（i=1，2，…）等，由于随机事件是样本空间的子集，从而事件的关系与运算和集合的关系与运算完全相类似.

1.事件的包含关系

定义2

若事件A发生必然导致事件B发生，则称事件B包含了A，或称A是B的特款，记作A⊂B或B⊃A.

比如前面提到过的A={球的标号为6}，这一事件就导致了事件B={球的标号为偶数}的发生，因为摸到标号为6的球意味着偶数的球出现了，所以A，B⊂Ω可以给上述含义一个几何解释，设样本空间是一个正方体，A，B是两个事件，也就是说，它们是Ω的子集，“A发生必然导致B发生”意味着属于A的样本点在B中由此可见，事件A⊂B的含义与集合论是一致的.

特别地，对任何事件A，有A⊂ΩA⊂Ω∅⊂A

2.事件的相等

设A，B⊂Ω，若A⊂B，同时有B⊂A，称A与B相等，记为A=B，易知相等的两个事件A，B总是同时发生或同时不发生，在同一样本空间中两个事件想等意味着它们含有相同的样本点.

3.并（和）事件与积（交）事件

定义3

设A，B⊂Ω，称事件“A与B中至少有一个发生”为A和B的和事件或并事件，记作A∪ B.

实质上A∪B“A或B发生”.

若A⊂B，则A∪B=B，A⊂A∪B，B⊂A∪ B.(www.xing528.com)

例3 设某种圆柱形产品，若底面直径和高都合格，用事件表示则该产品不合格.

解 令A={直径不合格}，B={高度不合格}，则A∪B={产品不合格}.

定义4

设A，B⊂Ω，称“A与B同时发生”这一事件为A和B的积事件或交事件.

记作A·B或A∩ B.

显然A∩∅=∅，A∩Ω=A，A∩A=A，A∩B⊂A，A∩B⊂ B.

若A⊂B，则A∩B=A.

如例3中，若C={直径合格}，D={高度合格}，则C·D={产品合格}.

4.差事件

定义5

设A，B⊂Ω，称“A发生B不发生”这一事件为A与B的差事件，记作A- B.

如例3中A-B={该产品的直径不合格，高度合格}，明显地有A-B=A-AB，A=∅=A

5.对立事件

定义6

称“Ω-A”为A的对立事件或称为A的逆事件，记作.

由此说明，在一次试验中A与有且仅有一个发生.

即不是A发生就是发生.

例4 设有100件产品，其中5件产品为次品，从中任取50件产品.若A={50件产品中至少有一件次品}，问表示什么？

解 记A={50件产品中至少有一件次品}，

则={50件产品中没有次品}={50件产品全是正品}.

由此说明，若事件A比较复杂，往往它的对立事件比较简单，因此我们在求解复杂事件的概率时，往往可能转化为求它的对立事件的概率.

6.互不相容事件（互斥事件）

定义7

若两个事件A与B不能同时发生，即AB=∅，称A与B为互不相容事件（或互斥事件）.

注意 任意两个基本事件都是互斥的.

7.事件的运算法则

（1）交换律 A∪B=B∪A，AB=BA；

（2）结合律 （A∪B）∪C=A∪（B∪C），（AB）C=A（BC）；

（3）分配律 （A∪B）∩C=（A∩C）∪（B∩C）

(A∩B)∪C=(A∪C)∩(B∪C);

（4）对偶原则.

不难发现，概率中事件的运算和集合的运算具有相互对关系见表9-1.

表9-1 事件的运算和集合的运算的关系

例5 设A，B，C为Ω中的随机事件，试用A，B，C表示下列事件.

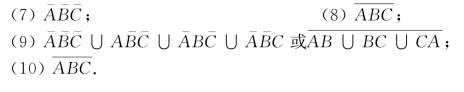
课后提升

1.从1，2，3这三个数中，每次取一个，一共取两次，分为有放回、无放回，分别写出随机试验的样本空间.

2.设A，B，C分别表示三个事件，用A，B，C以及表示下列事件.

（1） 只有事件B发生；

（2）A，B，C中不多于一个发生.

答案

1.有放回：Ω={（1，1），（1，2），（1，3），（2，1），（2，2），（2，3），（3，1），（3，2），（3，3）}.

无放回：Ω={（1，2），（1，3），（2，1），（2，3），（3，1），（3，2）}.

2.(1);(2).