【摘要】:作变换y′=m(x),则y″=m′(x),则方程(8.4.2)可变形为m′(x)=f(x,m),式中m(x)即代表未知函数的一阶微分方程,求出m(x)的解.m(x)=φ(x,c),即y′=φ(x,c),则方程(8.4.2)的通解为例3 求解微分方程y″(1+ex)=exy′的通解.解 设y′=m(x),则y″=m′(x).将y′与y″代入原方程后可得m′(x)(1+ex)=exm(x),即将该方程
作变换y′=m(x),则y″=m′(x),则方程(8.4.2)可变形为m′(x)=f(x,m),式中m(x)即代表未知函数的一阶微分方程,求出m(x)的解.m(x)=φ(x,c),即y′=φ(x,c),则方程(8.4.2)的通解为
例3 求解微分方程y″(1+ex)=exy′的通解.
解 设y′=m(x),则
y″=m′(x).
将y′与y″代入原方程后可得
m′(x)(1+ex)=exm(x),
即
将该方程分离变量得
两端同时积分得
求解得
lnm =ln(1+ex)+lnC,
即
m=C(1+ex ).
从而,有y′=C(1+ex),再对其积分可得原方程的通解为y=C(x+ex)+C1.
MATLAB解法如下:
例4 求解微分方程y″(1+sinx)=y′cosx在y|x=0=1,y′|x=0=2的特解.
解 设y′=m(x),则
y″=m′(x).
将y′与y″代入原方程后可得
m′(x)(1+sinx)=m(x)cosx,
即
两端同时积分可得(https://www.xing528.com)
lnm =ln(1+sinx)+lnC,
即
m(x)=C(1+sinx),
即
y′=C(1+sinx).
两端同时积分可得
y=C(x-cosx)+C1.
将初始条件y|x=0=1,y′|x=0=2代入y′与y″可得:C=2,C1=3,
该方程的特解为
y=2(x-cosx)+3.
MATLAB解法如下:
课后提升
1.求解下列微分方程的通解.
(1)y‴=sin(-x)-2x;(2)y‴=ex+3.
2.求微分方程满足初始条件的特解.
(1)y″=x+ex,y|x=0=2,y′|x=0=1;
(2)![]() .
.
答案
1.(1)![]() ;(2)
;(2)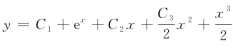 .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




