一阶非齐次线性微分方程解法

通过上述方法，可求得一阶线性齐次微分方程的通解为y=（C为任意常数）.假设一阶线性非齐次微分方程也存在类似的通解，而其中的C不是任意的常数，而是一个关于x的函数，设这个函数为q（x）.

马尔萨斯人口预测模型

接下来，我们讨论这样的函数q（x）是否存在，使得为非齐次微分方程的通解.

假设就是非齐次微分方程的解.

对两端求导得

将y与y′代入原方程，得

即

两端同时积分，得

故这样的q（x）存在，将上式代入，则非齐次微分方程p（x）y=Q（x）的通解为：

或者

式（8.3.5）中的右端第一项是对应的齐次微分方程的通解，第二项是线性非齐次微分方程通解公式（8.3.4）和式（8.3.5）中取C=0得到的一个特解.因此，一阶线性非齐次微分方程的通解等于它的一个特解以及与之对应的齐次微分方程的通解之和.

我们将一阶线性齐次微分方程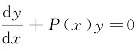的通解中的任意常数C换成待定的函数q（x），然后求出对应的一阶线性非齐次微分方程通解的方法，称为常数变易法.

例1 求解微分方程y′-2xy=ex2的通解.

解 解法一（常数变易法）

（1）求对应齐次微分方程y′-2xy=0的通解.

（2）设y=q（x）ex2为原线性非齐次微分方程的通解.

解 解法二（公式法）

将代入一阶线性非齐次微分方程的通解公式得：(www.xing528.com)

MATLAB解法如下：

例2 求微分方程在y|x=0=1的特解.

解 用公式法有

p(x)=3,Q(x)=e3x.

则有

将y|x=0=1代入上式求得.

故该微分方程的特解为.

MATLAB解法如下：

课后提升

1.求微分方程通解.

(1)y′-y=2;(2);(3)y′+3xy=2x.

2.求微分方程y′+y=e-2x满足初始条件y|x=0=2的特解.

3.设一曲线方程过点（0，2），且该曲线在任意点的斜率等于ex+2y，求该曲线方程.

答案

1.(1)y=Cex-2;(2)y=e-x+Ce-2x;(3);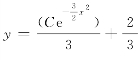

2.y=3e-x-e-2x.

3.y=3e2x-ex.