了解常微分方程迅速从高职应用数学下册中获得所需成果！

案例1 一曲线通过点（1，2），且在该曲线上任一点M（x，y）处的切线的斜率为2x，求这曲线的方程.

解 设所求曲线的方程为y=f（x）.根据导数的几何意义，可知未知函数y=f（x）应满足关系式

此外，未知函数y=f（x）还应满足下列条件：

把式（8.1.1）两端积分，得

把式（8.1.2）代入式（8.1.3），得

2=12+ C.

由此得出C=1.把C=1代入式（8.1.3），即得所求曲线方程

MATLAB解法如下：

案例2 将质点以初速度v0垂直向上抛出，不计阻力.试求其运动规律.

解 为了描述这个运动，取质点运动时所沿的垂直于地面的直线为x轴，x轴与地面的交点O为坐标原点建立直角坐标系，且规定背离地心的方向为x轴的正向.如图8-1所示.

设质点在时刻t的位置坐标为x（t），于是质点运动的瞬时速度v和瞬时加速度g可分别表示为

此外，x（t）还应满足下列条件：

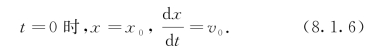
图8-1

把式（8.1.5）两端对t积分一次，得

再积分一次，得

把条件式（8.1.6）带入式（8.1.7）、式（8.1.8）中，得C1=v0，C2=x0

于是有

这就是上抛运动规律x=x（t）所满足的运动规律.

关系式和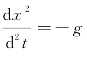都含有未知函数的导数，它们都是微分方程.

微分方程的概念

定义1

一般地，把含有未知函数的导数（或微分）的方程，称为微分方程；有时简称方程.

1.常微分方程和偏微分方程

定义2

微分方程的判别举例

在微分方程中只含有一个自变量的方程称为常微分方程；有两个或两个以上自变量的方程称为偏微分方程.

2.一阶与高阶微分方程

定义3

在微分方程中，所含未知函数导数的最高阶数，称为该微分方程的阶.当n=1时，称为一阶微分方程，当n＞1时，称为高阶微分方程.

一阶常微分方程的一般显性形式为：y′=f（x，y）.

一阶常微分方程的一般隐性形式为：F（x，y，y′）=0.

n阶显性方程的一般形式为：y（n）=f（x，y，y′，y″，…，y（n-1））.

n阶隐性方程的一般形式为：F（x，y，y′，y″，…，y（n））=0.

例如，方程和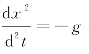分别为一阶、二阶常微分方程.

方程y（4）-4y+10y″-5y′=sinx是四阶微分方程.

3.线性和非线性微分方程

定义4

如果微分方程F（x，y，y′，y″，…，y（n））=0的左端为未知函数及其各阶导数的一次有理整式，则称为线性微分方程，否则称为非线性微分方程.

n阶线性微分方程的一般形式为a0（x）y（n）+a1（x）y（n-1）+…an（x）y=g（x）.其中a0（x）≠0，a0（x），a1（x），…，an（x），g（x）均为x的已知函数.

4.方程的解

定义5

对于微分方程F（x，y，y′，y″，…，y（n））=0，若将函数y=φ（x）代入方程后使其有意义且两端相等，即F（x，φ（x），φ′（x），…，φ（n）（x））≡0，则称函数y=φ（x）为该方程的一个显式解.若方程的解是某关系式的隐函数，则称这个关系式为该方程的隐式解.(www.xing528.com)

方程的显式解和隐式解统称为微分方程的解.

5.通解、特解、初始条件

定义6

常微分方程的解的表达式中，可能包含一个或者几个任意常数，若其所包含的独立的任意常数的个数恰好与该方程的阶数相同，称这样的解为该微分方程的通解.满足某些条件的解称为微分方程的特解.

设微分方程中的未知函数为y=y（x），如果微分方程是一阶的，通常用来确定任意常数的条件是：

其中x0，y0都是给定的值；如果微分方程是二阶的，通常用来确定任意常数的条件是：x=x0时，y=y0，（或）.

其中x0，y0及都是给定的值.上述这种用于确定通解中任意常数的条件，称为初始条件（或初值条件）.我们把满足初始条件的方程的解称为特解，也就是说，特解中不再包含任意常数.例如，案例1中，函数式（8.1.4）是微分方程满足初始条件的特解；案例2中，函数式（8.1.9）也是微分方程满足初始条件的特解.

6.初值问题

定义7

求微分方程y′=f（x，y）满足初始条件解的问题，叫做一阶微分方程的初值问题，记作y′=f（x，y），.

过定点的积分曲线：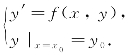

微分方程是我们解决实际问题的有利工具，现将利用微分方程解决实际问题的基本步骤总结如下：

（1）建立起实际问题的数学模型，也就是建立反映这个实际问题的微分方程；

（2）求解该微分方程的通解；

（3）依据题目中的初始条件确定该微分方程的特解；

（4）用数学结果解释实际问题，从而预测到某些物理过程的特定性质，以便达到能动地改造世界，解决实际问题的目的.

例1 验证函数y=C1cos2x+C2sin2x是微分方程y″+4y=0的通解.其中C1，C2是任意常数，并求满足初始条件y|x=0=1，y′|x=0=-1的特解.

解 因为y=C1cos2x+C2sin2x，

故y′=-2C1sin2x+2C2cos2x，

y″=-4C1cos2x-4C2sin2x.

将y，y′，y″代入原方程y=C1cos2x+C2sin2x中，得

-4C1cos2x-4C2sin2x+4C1cos2x+4C2sin2x=0.

故已给函数满足方程y″+4y=0，是它的解.又因为这个解中含有两个独立的任意常数，等于方程y″+4y=0的阶数，因此又是它的通解.

将初始条件y|x=0=1，y′|x=0=-1代入y，y′两式中，得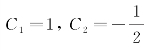.得所求的特解为.

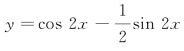MATLAB解法如下：

例2 验证函数y=C1ex+C2e2x（C1，C2为任意常数）为二阶微分方程y″-3y′+2y=0的通解.

解 y=C1ex+C2e2x，

y′=C1ex+2C2e2x,

y″=C1ex+4C2e2x.

将y，y′，y″代入方程y″-3y′+2y=0左端，得

C1ex+4C2e2x-3(C1ex+2C2e2x)+2(C1ex+C2e2x)

=(C1-3C1+2C1)ex+(4C2-6C2+2C2)e2x=0.

所以，函数y=C1ex+C2e2x是所给微分方程的解.又因为，这个解中有两个独立的任意常数，与方程的阶数相同，所以它是所给微分方程的通解.

课后提升

1.指出下列方程中，哪些是微分方程？并说出它们的阶数.

2.下面几种说法对吗？为什么？

（1）自变量个数不只有一个的微分方程称为常微分方程；

（2）含有两个任意常数的解必是二阶微分方程的通解.

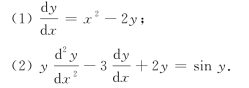
3.指出下面微分方程的阶数，并回答是否线性的.是否为微分方程（x+y）dx=-xdy的相应解？若是解，说明是通解还是特解（其中C1，C2是任意常数）.

5.求下列微分方程满足所给初始条件的特解.

4.验证

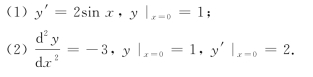
答案

1.（1）不是；（2）是 一阶；（3）是 二阶；（4）是 四阶.

2.（1）错；（2）错.

3.（1）一阶 线性；（2）二阶 非线性.

4.是 通解.

5.(1)y=3-2cos(x);(2).