求解牛顿-莱布尼茨公式：高职应用数学下册

定积分的定义已经给出了定积分的计算方法.即通过“分割”、“近似代替”、“求和”、“取极限”的步骤，求出函数f（x）的定积分.但是这种方法计算复杂，一般来说，实际意义不大.我们试图寻找一种简便、实用、有效的计算方法.

7.2.2.1 变上限函数（也叫积分上限函数）

设函数f（x）在区间[a，b]上连续，对任意t∈[a，b]，定积分

表示曲边梯形的面积.若x是区间[a，

b]上任意一点，定积分

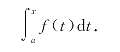
表示f（x）在部分区间[a，x]上曲边梯形的面积（图7-16）.当x在区间[a，b]上变化时，阴影部分的曲边梯形面积也跟着在变化，所以，变上限定积分

是上限变量x的函数.

显然，对任意x∈[a，b]，都对应唯一一个定积分（数）.根据函数定义，它是定义在区间[a，b]上的函数，表示为Φ（x），即

图7-16

定义 若函数f（x）在区间[a，b]上连续，那么在区间[a，b]上任取一点x，就有一个确定的定积分的值与之对应，把这个新的函数，称为变上限函数，记作Φ（x），即

类似的，还可定义变下限函数：

这里，变上限函数与变下限函数通称为变限函数.这里，我们主要介绍变上限函数的有关知识.

定理1 若函数f（x）在区间[a，b]上连续，那么变上限函数在区间[a，b]上可导，且Φ′（x）=f（x）.

证明 只须说明，对任意x∈[a，b]，有即可.

设x有改变量Δx，使x+Δx∈[a，b]，有

根据积分中值定理得，在x与x+Δx之间至少存在一点ξ，使

成立（图7-17）.

已知函数f（x）在区间[a，b]上连续，当Δx→0时，有ξ→x，f（ξ）→f（x）所以，，

即

Φ′(x)=f(x).

这个定理告诉我们：若函数f（x）在区间[a，b]上连续，那么变上限函数是f（x）的一个原函数，肯定了连续函数的原函数是存在的.

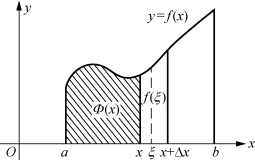
图7-17

定理2（原函数存在定理）如果函数f（x）在区间[a，b]上连续，那么变上限函数就是f（x）在该区间上的一个原函数.

例1 已知，求Φ′（x）.

解 由定理1可知，.

例2 已知，求Φ′（x）.

解 由定理1可知，.

例3 已知，求Φ′（x）.

解 上限x2是x的函数，所以变上限定积分是x的复合函数，由复合函数求导法则，得

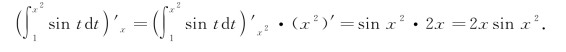
通过以上讨论有：

（1）如果函数f（x）在区间[a，b]连续，则有.

（2）如果函数f（x）在区间[a，b]上连续，φ（x）可导，则有

7.2.2.2 牛顿-莱布尼茨公式

定理3 若函数f（x）在区间[a，b]连续，且F（x）是f（x）的原函数，则

证明 已知F（x）是f（x）的原函数，即对任意x∈[a，b]，有(www.xing528.com)

F′(x)=f(x).

根据定理1，积分上限函数也是f（x）的原函数，于是

F(x)-Φ(x)=C (a≤x≤b),

即

Φ(x)=F(x)- C.

当x=a时，上式为Φ（a）=F（a）-C而，所以，F（a）=C从而

Φ（x）=F（x）-F（a），即

当x=b时，有将积分变量换成x，有

式（7.2.2）称为牛顿-莱布尼茨公式.它是积分学中的基本公式.这个公式揭示了定积分与不定积分之间的关系：定积分的值等于被积函数的任一原函数在积分区间上的增量.有了微积分基本公式，计算连续函数的定积分问题就转化为求被积函数的原函数，使计算变得更简单了.为了使用方便，还可以将公式写成下面的形式：

或

例1 计算.

解

MATLAB代码为：

按Enter得到结果为ans=1/3.

例2 计算.

解

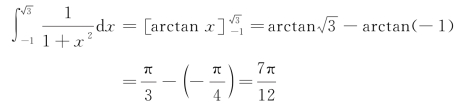
MATLAB代码为：

按Enter得到结果为ans=（7*pi）/12.

例3 计算.

解 .

MATLAB代码为：

按Enter得到结果为ans=-log（3）.

课后提升

1.选择题

（1）变上限积分是（ ）.

A.f′（x）的一个原函数 B.f′（x）的全体原函数

C.f（x）的一个原函数 D.f（x）的全体原函数

（2）设a为常数，且，则a=（ ）.

A.1 B.2 C.-1 D.-2

（3）设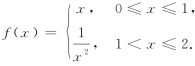则=（ ）.

A.1 B.-1 C.0 D.22

（4）下列各积分中，计算正确的是（ ）.

2.求下列函数的导数.

3.计算下列定积分.

答案