
积分思想初体验之曲边梯形的面积
7.2.1.1 定积分的概念
引例1 曲边梯形的面积
在生产实践活动中,有些问题的计算经常归结为求曲边图形的面积.而计算曲边图形的的面积又归结为计算曲边梯形的面积.
1.什么是曲边梯形
设函数f(x)在区间[a,b]上连续且f(x)≥0,由曲线y=f(x)和直线x=a,x=b以及y=0所围成的平面图形就称为曲边梯形.
如图7-3所示.ABCD就是一个曲边梯形.其中曲线段DC为曲边梯形的曲边,在x轴上的线段AB为曲边梯形的底边.
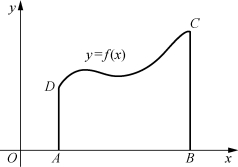
图7-3
2.怎样计算曲边梯形的面积呢
在初等数学中,我们已经知道了三角形、矩形、正方形及圆的面积公式.其中矩形的面积=底×高,这里,矩形的高是不变的.而由曲线y=f(x)和直线x=a,x=b以及x轴所围成的平面图形(图7-4)的面积取决于这个区间上的函数f(x)及区间[a,b].
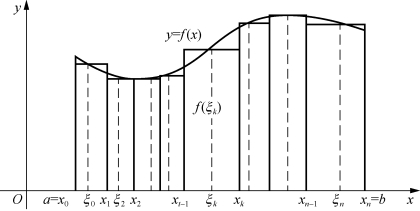
图7-4
如果f(x)在区间[a,b]上是常函数m,这时的曲边梯形为矩形,其面积等于底×高即m×(b-a).现在的问题是函数f(x)在区间[a,b]上不是常函数,曲边梯形的高在区间[a,b]上是变动着的.它的面积不能简单的用矩形面积公式来计算.然而,由于f(x)是区间[a,b]上的连续函数,在很小一段区间上它的变化很小,近似于不变,且区间的长度无限减小时,高度的变化也无限减小.因此,我们如果将区间[a,b]分割成许多小区间,相应地,将曲边梯形分割成许多小曲边梯形,把每个小区间上对应的小曲边梯形近似地看成小矩形.所有的小矩形面积的和,就是整个曲边梯形面积的近似值.
显然,区间[a,b]分割愈细,近似程度愈好.因此,将区间[a,b]无限地细分,并使每个小曲边梯形的底边长都趋近于零,则小矩形面积之和的极限值就是曲边梯形面积的精确值.
根据上述分析,曲边梯形的面积可按下述步骤来计算:
(1)分割:在区间[a,b]内任意插入n-1个分点,把区间分成n个小区间,其分点是x1,x2,…,xn-1,令a=x0,b=xn,则a=x0<x1<…<xn-1<xn=b,第k个小区间可表示为[xk-1,xk],其长度记为
Δxk=xk-xk-1(k=1,2,3,…,n).
过各分点分别作垂直于x轴的直线段,把整个曲边梯形分成n个小曲边梯形其中第k个小曲边梯形的面积记为ΔAk(k=1,2,…,n).
(2)近似代替:在每个小区间[xk-1,xk]上任取一点ξk(xk-1≤ξk≤xk),以f(ξk)为高,Δxk为底的小矩形的面积为f(ξk)Δxk,则小曲边梯形面积ΔAk的近似值就是小矩形的面积.即
ΔAk≈f(ξk)Δxk (k=1,2,…,n).
(3)求和:把n个小曲边梯形面积的近似值相加,就得到所求曲边梯形面积A的近似值,即

(4)取极限:当每个小区间的长度Δxk都趋近于零时,和式![]() 的极限就是A的精确值.记所有小区间长度的最大值为
的极限就是A的精确值.记所有小区间长度的最大值为![]() ,当λ→0时,就有
,当λ→0时,就有

这样,计算曲边梯形面积的问题,就归结为求和式的极限.
引例2 变速直线运动的路程.
设一物体做直线运动,已知速度v=v(t)是时间t在区间[t1,t2]上连续函数,且v(t)≥0,计算在这段时间内该物体经过的路程.
物体做变速直线运动就不能用匀速直线运动那样用速度乘以时间求路程,因速度是变化着的.即速度v(t)随着时间t的变化而变化.但是,若把时间区间[t1,t2]分成许多小时间区间段,由于物体运动的速度是连续变化的,则在每个小段时间内,速度变化不大,可以近似地看作是匀速的(图7-5).于是,可以用类似于求曲边梯形面积的方法计算路程.
![]()
图7-5
具体的步骤也可以分为以下四部:
(1)分割:在时间区间[a,b]内任意插入n-1个分点,把区间分成n个小区间,其分点是t1,t2,…,tn-1,令a=t0,b=tn,则a=t0<t1<…<tn-1<tn=b,第k个时间小区间可表示为[tk-1,tk],其长度记为
Δtk=tk-tk-1(k=1,2,3,…,n).
相应的路程s被分为n个小路程:Δsk(k=1,2,3,…,n).
(2)近似代替:在每个小区间[tk-1,tk]上任取一点ξk(xk-1≤ξk≤xk),用任意时刻ξk的速度v(ξk)来近似代替小区间的速度.用v(ξk)·Δtk近似代替物体在小区间[tk-1,tk]上的路程Δsk.从而得到物体在第k段时间[tk-1,tk]内所经过的路程Δsk的近似值.即
Δsk≈v(ξk)Δtk.
(3)求和:把n段时间上的路程的近似值相加,就是时间区间[a,b]上的路程s的近似值.即

(4)取极限:当每个小区间的长度Δtk都趋近于零时,和式 的极限就是s的精确值.记所有小区间长度的最大值为
的极限就是s的精确值.记所有小区间长度的最大值为![]() ,当λ→0时,就有
,当λ→0时,就有
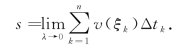
由此可见,变速直线运动的路程也是一个和式的极限.
上面讨论的两个实际问题可以看出,虽然它们的实际意义不同,但解决问题的思想方法和步骤是相同的,最后都归结为求函数在某一区间上的一种特定结构和式的极限.
7.2.1.2 定积分的定义
设函数f(x)在区间[a,b]上有定义,用分点a=x0<x1<…<xn-1<xn=b,把区间[a,b]分为n个小区间[xk-1,xk],其长度为
Δxk=xk-xk-1 (k=1,2,3,…,n).
在每个小区间[xk-1,xk]上任取一点ξk(xk-1≤ξk≤xk),并作乘积
f(ξk)Δxk (k=1,2,3,…,n).
及和式

如果不论对区间[a,b]怎么分法,也不论在小区间[xk-1,xk]上的点ξk怎样取法.令![]() ,当λ→0时,如果和式
,当λ→0时,如果和式![]() 的极限存在,则称此极限值为函数f(x)在区间[a,b]上的定积分,记作
的极限存在,则称此极限值为函数f(x)在区间[a,b]上的定积分,记作![]() ,即
,即
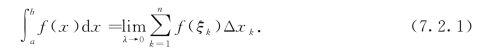
式(7.2.1)中,f(x)叫做被积函数,f(x)dx叫做被积表达式或被积分式,x叫做积分变量,区间[a,b]叫做积分区间,a与b分别叫做积分下限与积分上限,![]() 叫做积分号.
叫做积分号.
根据定积分的定义,引例1,引例2可以表示为
曲边梯形的面积

变速直线运动的路程
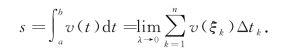
理解:定积分的定义需要注意的问题:
(1)定积分是一种特定结构和式的极限,是一个数,这个数只与被积函数f(x)及积分区间[a,b]有关.与区间[a,b]的分割方法无关,与点ξk的选取无关,与积分变量的记号无关.即

(2)该定义是在a≠b,且a<b的情况下给出的,当a=b及a>b时,为了运算的需要,规定
当a=b时,![]() ,
,
当a>b时,![]() .
.
对于定积分有这样的问题,函数f(x)在什么条件下,定积分存在?我们给出下面的结论:
①函数f(x)在闭区间[a,b]上连续,则f(x)在区间[a,b]上可积.
②函数f(x)在闭区间[a,b]上是单调的,则f(x)在区间[a,b]上可积.
③函数f(x)在闭区间[a,b]上有界,且有有限个不连续点,则f(x)在区间[a,b]上可积.
如初等函数在其定义域上连续,则初等函数在其定义域上都可积.
7.2.1.3 定积分的几何意义
由定积分的定义,可以得出定积分几何意义:
(1)如果函数f(x)区间[a,b]上连续且f(x)≥0,那么定积分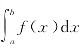 等于由连续曲线y=f(x)和直线x=a,x=b以及x轴所围成的曲边梯形的面积(图7-6).即
等于由连续曲线y=f(x)和直线x=a,x=b以及x轴所围成的曲边梯形的面积(图7-6).即

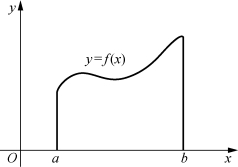
图7-6
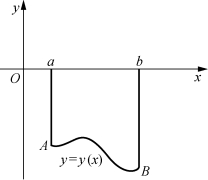
图7-7
(2)如果函数f(x)区间[a,b]上连续且f(x)<0,这时的曲边梯形在x轴的下方,f(ξk)<0,和式的极限值小于零(图7-7),即
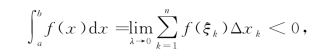
这时
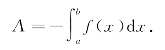
(3)如果函数f(x)区间[a,b]上连续,且有时为正有时为负时,那么定积分![]() 等于由连续曲线y=f(x)和直线x=a,x=b以及x轴所围成的几个曲边梯形面积的代数和(图7-8).即
等于由连续曲线y=f(x)和直线x=a,x=b以及x轴所围成的几个曲边梯形面积的代数和(图7-8).即
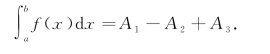
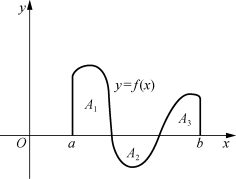
图7-8
例1 用定积分表示(图7-9)中阴影部分的面积.
解 如图7-9所示,被积函数 在(1,2]上连续,且y>0.由定积分的几何意义可得阴影部分的面积为
在(1,2]上连续,且y>0.由定积分的几何意义可得阴影部分的面积为
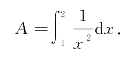
 (https://www.xing528.com)
(https://www.xing528.com)
图7-9
例2 用定积分的几何意义计算定积分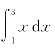 的值.
的值.
解 如图7-10所示,被积函数y=x在[1,3]上连续,且y>0.由定积分的几何意义可知,计算定积分![]() 就是计算由直线y=x,x=1,x=3以及x轴所围成的梯形的面积.所以
就是计算由直线y=x,x=1,x=3以及x轴所围成的梯形的面积.所以
![]()
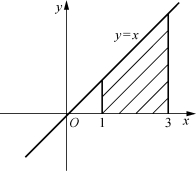
图7-10
7.2.1.4 定积分的性质
性质1 若函数f(x)与g(x)在[a,b]上可积,则f(x)+g(x)在[a,b]上也可积,且

性质1,可推广到有限个函数代数和的情况,即
![]()
性质2 若函数f(x)在[a,b]上可积,则cf(x)在[a,b]上也可积,且
![]()
性质3 若在区间[a,b]上,f(x)=c(常数),则f(x)=c在[a,b]上可积,且
![]()
性质4(积分区间的可加性) 若函数f(x)在区间[a,c]与[c,b]上可积,则f(x)在[a,b]上也可积,且
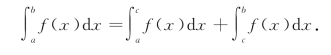
因为作积分和时,无论将[a,b]如何划分,积分和的极限总是不变的,所以我们在划分区间时,把c作为分点,则
(1)当c在区间[a,b]内(图7-11)时,由定积分的几何意义可知

图7-11

图7-12
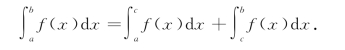
(2)当c在区间[a,b]外时(图7-12),不妨设a<b<c,由定积分的几何意义可知

移项,得

而
![]()
所以
![]()
类似地,若c<a<b时,也可以得出相同的结果.
性质5 若函数f(x)在区间[a,b]上可积,且对任意x∈[a,b],有f(x)≥0(或f(x)≤0),则

性质6 若函数f(x)与g(x)在[a,b]上可积,且对任意x∈[a,b],有f(x)≤g(x),
则

性质7(估值不等式)若函数f(x)在区间[a,b]上的最大值为M,最小值为m,则
![]()
例 试估计定积分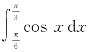 的值.
的值.
解 在区间 上,函数f(x)=cosx是减函数,且最大值
上,函数f(x)=cosx是减函数,且最大值

最小值

由性质7可知,

即

性质8(积分中值定理)若函数f(x)在区间[a,b]上连续,则在[a,b]上至少存在一点ξ,使
![]()
该性质的几何解释是:
(1)在区间[a,b]上,若f(x)≥0,由连续曲线y=f(x)和直线x=a,x=b以及x所所围成的曲边梯形的面积等于以[a,b]上某一点ξ对应的函数值f(ξ)作为高,以区间[a,b]的长作为宽的矩形的面积(图7-13).

图7-13
(2)函数f(x)在区间[a,b]上的平均值为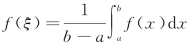 .该性质解决了连续函数求平均值的问题.
.该性质解决了连续函数求平均值的问题.
如:西安2009年4月8日从0到24时气温变化曲线为y=f(t),t为时间,则这天的平均气温为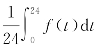 .
.
课后提升
1.已知电流i与时间t的函数关系i=i(t).用定积分表示从时刻0到时刻t这一段时间流过导线横截面的电荷量.
2.由曲线y=x3,直线x=1,x=4及x轴围成的曲边梯形,试用定积分表示该曲边梯形面积A.
3.利用定积分的几何意义计算定积分.
![]()
4.用定积分表示下列各图中阴影部分的面积(图7-14).

图7-14
5.选择题
(1)定积分![]() 的结果是( ).
的结果是( ).
A.f(x)的一个原函数 B.任意常数1
C.f(x)的全体原函数 D.确定的常数
(2)已知变速直线运动物体的速度为v(t)≥0,则物体从时刻t1到时刻t2走过的路程为( ).
![]()
(3)根据定积分的几何表示,下列各式正确的是( ).
![]()
![]()
(4)观察下面的图形(图7-15),将各题中的正确答案的代号填写在题后的括号内.
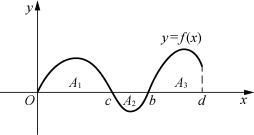
图7-15
①定积分![]() 的结果是( ).
的结果是( ).
A.A1+A2 B.A1-A2 C.A2-A1 D.A1+A3-A2
②定积分![]() 的结果是( ).
的结果是( ).
A.A2+A3 B.A2-A3 C.A3-A2 D.A1+A3-A2
③定积分![]() 的结果是( ).
的结果是( ).
A.A1+A2+A3 B.A1+A2-A3 C.A1+A3-A2 D.A2+A3-A1
6.利用定积分的性质和![]() ,计算下列各定积分.
,计算下列各定积分.
![]()
7.计算不定积分的值,说明下列积分哪一个较大.
![]()
答案

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




