如何计算不定积分-高职应用数学　下册

利用积分的基本公式和积分法则所能计算的不定积分是非常有限的.因此，有必要进一步研究不定积分的求法.本节我们将介绍换元积分法，分部积分，MATLAB计算积分.

换元积分法简称换元法.换元法的基本思路是：利用变量替换，使得被积表达式变形为基本公式表中的积分形式，进而计算不定积分.换元法有两类：第一类换元法；第二类换元法.

换元积分法解决了许多函数的不定积分问题，但是，还有一部分函数如：等的不定积分，不能用换元法解决.因此，有必要介绍求积分的另一种方法分部积分法.

对于一些复杂积分计算问题，用MATLAB积分进行计算.

7.1.2.1 换元积分法

1.第一类换元法（凑微分法）

定理 设，若u=φ（x）连续可导，则有

从这个定理我们看到：如果要求的积分能写成

的形式，则令φ（x）=u后，求出，再代入u=φ（x）就行了.即

通常把这样的积分方法叫做第一类换元法.

例1 求.

解 设u=2x，则du=2dx.根据公式（7.1.2），有

MATLAB代码为：

例2 求.

解 设u=3-5x，则du=-5dx.根据公式（7.1.2），有

MATLAB代码为：

例3 求.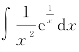

解 设，则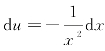.根据公式（7.1.2），有

方法熟练之后，可以不用写出换元过程，使计算简便.

MATLAB代码为：

如例1，例2，例3可直接写成：

从上面的例子可以看出，求积分时经常用到微分性质.

(1)d[aφ(x)]=adφ(x);(2)dφ(x)=d[φ(x)±b].

用第一类换元法计算积分时，关键是把被积表达式凑成两部分，使其中一部分为dφ（x），另一部分为φ（x）的函数f[φ（x）].因此，第一类换元法又称为凑微分法.

例4 求.

解 .

2.第二类换元法

在第一类换元法中，选择新变量u，令u=φ（x）进行了换元.但对一些无理函数的积分，如等就需要用第二类换元法.

定理 设f（x）连续，x=φ（t）及φ′（t）均连续，x=φ（t）的反函数x=φ′（t）存在，如果Φ（t）是f[φ（t）]φ′（t）的一个原函数，即

则

通常把这样的积分方法叫做第二类换元法.

第二类换元法的关键是选择合适的换元x=φ（t）.下面用具体例子说明.

例1 求.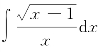

解 令，则x=t2+1 （t＞0）.于是dx=2tdt，所以

MATLAB代码为：

按Enter得到结果为ans=2*（x-1）^（1/2）-2*atan（（x-1）^（1/2））.

7.1.2.2 分部积分法

分部积分法

换元积分法解决了许多函数的不定积分问题，但是，还有一部分函数如：等的不定积分，不能用换元法解决.因此，有必要介绍求积分的另一种方法分部积分法.

设函数u=u（x）及v=v（x）具有连续导数.那么，两个函数乘积的导数为

(uv)′=u′v+uv′，

移项得由不定积分法则与不定积分定义，得

uv′=(uv)′-u′v.

或

式（7.1.3）或式（7.1.4）称为分部积分公式.

注意 分部积分公式的作用在于，如果右边的积分比左边的积分容易求得，那么这个公式就起到了化繁为减的作用.

通过下面的例子来具体说明，如何运用分部积分公式.

例1 求.

解 设u=x，dv=cosxdx=d（sinx）.则

du=dx,v=sinx.

由分部积分公式得

MATLAB代码为：(www.xing528.com)

按Enter得到结果为ans=cos（x）+x*sin（x）.

例2 求.

解 设u=x，dv=exdx=d（ex）.则

du=dx,v=ex.

由分部积分公式得

MATLAB代码为：

按Enter得到结果为ans=exp（x）*（x-1）.

在例2中，如果设.则

由分部积分公式得

很显然，右边的积分比左边的积分更不容易求出.由此可见，恰当的选取u和dv是应用分部积分法的关键.选取u和dv要注意以下两点：

（1）v要容易求得；

（2）要比容易积出.

一般的，形如下列函数

xklnx,xksinax,xkcosbx,xkeax,

xkarcsinax,xkarctanax

等等的不定积分，就要用分部积分法解决.

例3 求.

解 设u=arcsinx，dv=dx.则

由分部积分公式得

例4 求.

解 设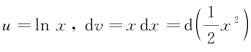.则

由分部积分公式得

MATLAB代码为：

按Enter得到结果为ans=（x^2*（log（x）-1/2））/2.

分部积分法的方法熟练后，可简化步骤.

7.1.2.3 MATLAB积分方法

手机下载MATLAB Mobile，并创建自己的MathworksClound，就可以使用了.

MATLAB中主要用int进行符号积分.

int(s,

v）：对符号表达式s中指定的符号变量v计算不定积分.表达式R只是表达式函数s的一个原函数，后面没有带任意常数 C.

int（s）：对符号表达式s中确定的符号变量计算不定积分.

例1 用符号积分命令int计算不定积分.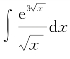

MATLAB代码为：

按Enter得到结果为ans=（2*exp（3*x^（1/2）））/3.

所以.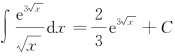

其中，clear指令为清除内存变量，分号“；”表示语句结束，隐藏运算结果symsx为定义符号变量x.

例2 求.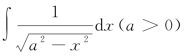

解 MATLAB代码为：

按Enter得到结果为ans=asin（x/a）.

例3 求.

解 MATLAB代码为：

按Enter得到结果为ans=log（sin（x））.

所以.

课后提升

1.填空

2.求下列不定积分.

3.求下列不定积分.

答案