不定积分的概念与性质-高职应用数学下册

7.1.1.1 原函数与不定积分

1.原函数

原函数和不定积分的定义

物理学中如果已知物体的运动规律（函数）是s=s（t），其中t是

时间，s是物体运动的距离，则导数s′（t）=v（t）是物体在时间t的瞬时速度.但是，有时要遇到相反的问题，就是已知物体的瞬时速度v（t）[即s′（t）]，求物体的运动规律s（t）.从数学角度来说，这个相反问题的实质是：要找一个函数s=s（t），使得它的导数s′（t）等于已知函数v（t），即s′（t）=v（t）.这种问题在数学及其应用中具有普遍的意义，值得我们讨论.

定义 设f（x）定义在区间D上，如果对任意的x∈D，都有F′（x）=f（x）或dF（x）=f（x）dx，则称F（x）为f（x）在该区间上的一个原函数.

例如，因为（x2）′=2x，所以2x是函数x2在R上的原函数；又因为

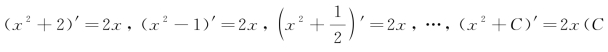为任意常数）所以x2，x2+2，x2-1，，x2+C等，都是2x的原函数.

研究原函数必须注意两个问题：

（1）在什么条件下，一个函数的原函数存在？如果存在，有几个？

（2）如果一个函数的原函数存在，怎样求出来？

对于第一个问题有下面的两个定理；第二个问题，则是本章重点介绍的几种积分方法.

定理1（原函数存在定理）如果函数f（x）在区间D上连续，那么f（x）在区间D上存在原函数F（x）.

由于初等函数在其定义域上都是连续的，所以，初等函数在其定义域上都有原函数.

定理2（原函数族定理）如果函数f（x）有原函数，那么它就有无限多个原函数，并且其中任意两个原函数只差一个常数.

事实上，设G（x）和F（x）是f（x）的任意两个原函数，那么G（x）-F（x）的导数（G（x）-F（x））′=G′（x）-F′（x）=f（x）-f（x）≡0，由于导数恒为零的函数必为常数，所以，G（x）-F（x）=C（C为任意常数），移项得G（x）=F（x）+ C.

这个定理表明，若F（x）是f（x）的一个原函数，则f（x）的全体原函数为F（x）+C（其中C为任意常数）.

2.不定积分

定义 函数f（x）在区间D上的全体原函数称为f（x）在区间D上的不定积分，记作

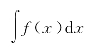
其中叫做积分号，f（x）叫做被积函数，f（x）dx叫做被积表达式，x叫积分变量.

由定义可知，如果F（x）是f（x）的一个原函数，那么f（x）的不定积分就是原函数族F（x）+C，即

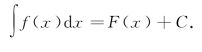
例1 求.

解 由于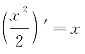，所以是x的一个原函数.因此，

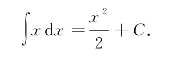
例2 求.

解 由于（-cosx′）=sinx，所以-cosx是sinx的一个原函数.因此，

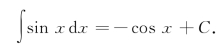
例3 求.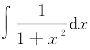

解 由于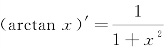，所以arctanx是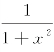的一个原函数.因此，

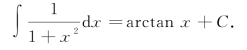
例4 求.

解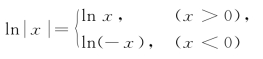

当x＞0时，有，所以lnx是的一个原函数.因此，

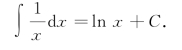
当x＜0时，有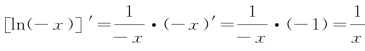，所以ln（-x）是的一个原函数.因此，

所以

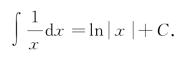
例5 求通过点（1，2），斜率为2x的曲线方程.

解 因为，所以斜率为2x的全部曲线为

即

而所求的曲线通过点（1，

2），代入式（7.1.1）得

2=1+C,C=1,

于是所求的曲线方程为

y=x2+1.

由解析几何可知：式（7.1.1）的图像由抛物线y=x2沿着y轴上下平移可得.当C＞0时，向上平移个单位；当C＜0时，向下平移个单位.因此式（7.1.1）的图像是一族抛物线（图7.1.1），而所求曲线y=x2+1是抛物线族中通过点（1，2）的那一条.

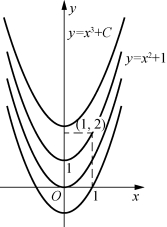
图7-1

7.1.1.2 不定积分的几何意义

一般的，如果F（x）是f（x）的一个原函数，则称y=F（x）的图像为f（x）的一条积分曲线.于是，函数f（x）的不定积分在几何上表示f（x）的某一条积分曲线沿纵轴方向平移所得一切积分曲线组成的曲线族.显然，若在每一条积分曲线上横坐标相同的点处做切线，则这些切线都是互相平行的（图7-2）.

7.1.1.3 不定积分的性质

性质1 或，

即不定积分的导数（或微分）等于被积函数（或被积表达式）.

事实上，设F（x）是f（x）的一个原函数，即F′（x）=f（x），则

性质2 或，

即函数F（x）的导数（或微分）的不定积分等于函数族F（x）+ C.

事实上，已知F（x）是F′（x）的原函数，则(www.xing528.com)

例如：

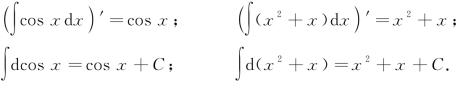
7.1.1.4 不定积分的运算法则与基本公式表

直接积分法习题讲解

1.不定积分的运算法则

法则1 ，（k是常数，且k≠0），

即被积函数的常数因子可以移到积分号的外边.

事实上，，

即.

法则2 ，

即两个函数代数和的不定积分等于每个函数不定积分的代数和.

事实上，，

即.

这个法则可推广到n个（有限）函数，即n个函数代数和的不定积分等于n个函数不定积分的代数和.

2.基本公式表

因为求不定积分的运算是求导数的逆运算，所以可得到不定积分的基本公式表：

基本公式表中所列的不定积分公式，是求不定积分不可缺少的，要求读者牢记会用.应用不定积分法则和不定积分公式可以求出一些简单的不定积分.

例6 求下列不定积分：

解 （1）.

MATLAB代码为：

按Enter得到结果为ans=-1/x.

(2).

MATLAB代码为：

按Enter得到结果为ans=-2/x^（1/2）.

例7 求.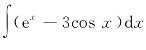

解

MATLAB代码为：

按Enter得到结果为ans =exp（x）-3*sin（x）.

课后提升

1.选择题

（1）某区间上，若F（x）是f（x）的一个原函数，C为任意常数，则下式成立的是（ ）.

A.F′(x)+C=f(x) B.F(x)dx+C=f(x)dx

C.(F(x)+C′)=f(x) D.F′(x)=f(x)+C

（2）下列选项中，哪个选项不是cos2x的不定积分（ ）.

A.（C为任意常数） B.sin2x+C（C为任意常数）

C.sinxcosx+C（C为任意常数） D.（C为任意常数）

（3）若，则f（x）=（ ）.

A.3x2-ex+cosx B.

C. D.3x2-ex-cosx

（4）设f（x）的原函数是，则f′（x）=（ ）.

A. B. C. D.

2.验证：函数F［x］=（ex-e-x）2与函数G［x］=（ex+e-x）2是同一函数的原函数.

3.求下列不定积分.

4.一质点作直线远动，已知其速度为v=sinωt，且.求时间为t时物体和原点间的距离.

5.已知曲线上任一点切线的斜率等于该点处横坐标平方的3倍，且该曲线经过点（0，1），求曲线方程.

6.已知f（x）的导数为，且当x=e3时，y=5，求f（x）.

答案

1.(1)C;(2)B;(3)A;(4) D.

2.略.

3.(1);(2);(3);(4);(5);(6);(7);(8).

4..

5.y=x3+1.

6.y=lnx+2.