高职应用数学（下册）-整数规划模型

6.3.3.1 整数规划模型

1.钢管下料问题

某钢管零售商从钢管厂进货，将钢管按照顾客的要求切割后售出，从钢管厂进货时得到的原料钢管都是19m.

（1）现在一客户需要50根4m、20根6m和15根8m的钢管.应如何下料最节省？

（2）零售商如果采用的不同切割模式太多，将会导致生产过程的复杂化，从而增加生产和管理成本，所以该零售商规定采用的不同切割模式不能超过3种.此外，该客户除需要（1）中的三种钢管外，还需要10根5m的钢管.应如何下料最节省.

问题（1）分析与模型建立：

首先分析1根19m的钢管切割为4m，6m，8m的钢管的模式，所有模式相当于求解不等式方程

4k1+6k2+8k3≤19

的整数解.但要求剩余材料

r=19-(4k1+6k2+8k3)＜4.

容易得到所有模式见表6-20.

表6-20 钢管切割模式 单位：m

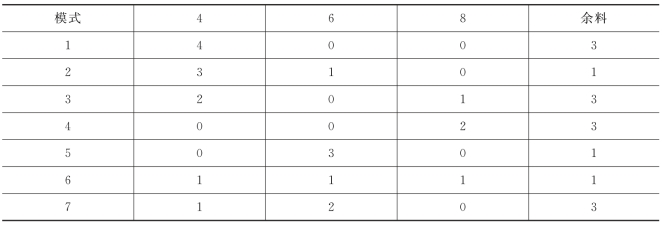
决策变量用xi表示按照第i种模式（i=1，2，…，7）切割的原料钢管的根数.以切割原料钢管的总根数最少为目标，则有

minz=x1+x2+x3+x4+x5+x6+x7.

约束条件

为满足客户的需求，4m长的钢管至少50根，有

4x1+3x2+2x3+x6+x7≥50.

6m长的钢管至少20根，有

x2+3x5+x6+2x7≥20.

8m长的钢管至少15根，有

x3+2x4+x6≥15.

因此模型为

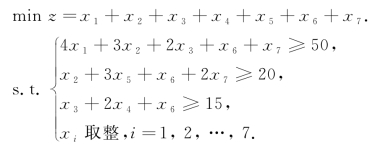
解得

x1=0,x2=12,x3=0,x4=0,x5=0,x6=15,x7=0.

目标值z=27.

即12根钢管采用切割模式2：3根4m，1根6m，余料1m.

15根钢管采用切割模式6：1根4m，1根6m，1根8m，余料1m.

切割模式只采用了2种，余料为27m，使用钢管27根.

LINGO程序：

问题（2）模型建立

首先分析1根19m的钢管切割为4m，6m，8m，5m的钢管的模式，所有模式相当于求解不等式方程

4k1+6k2+8k3+5k4≤19

的整数解.但要求剩余材料

r=19-(4k1+6k2+8k3)＜4.

利用MATLAB程序求出所有模式见表6-21.

表6-21 钢管切割模式 单位：m

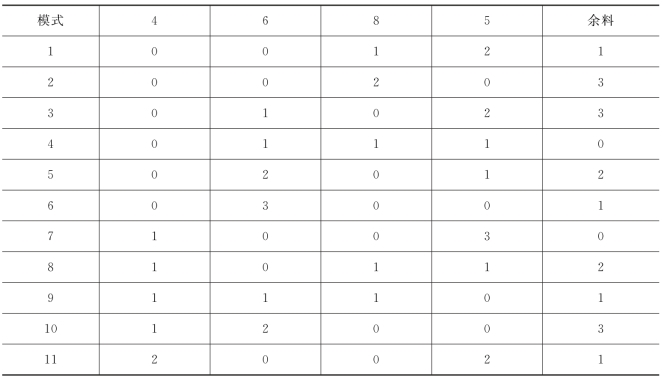
（续表）

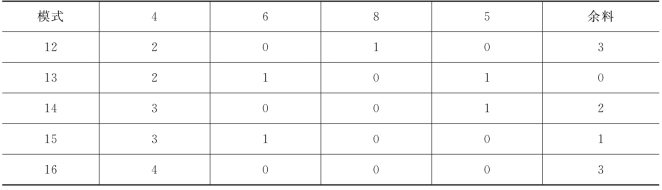
决策变量用xi表示按照第i种模式（i=1，2，…，16）切割的原料钢管的根数.

决策目标以切割原料钢管的总根数最少为目标，则有

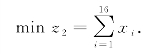
设第i种切割模式下4m长的钢管ai根，6m长的钢管bi根，8m长的钢管ci根，5m长的钢管di根.则约束条件有：

为满足客户的需求，4m长的钢管至少50根，有

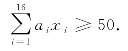
6m长的钢管至少20根，有

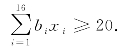
8m长的钢管至少15根，有

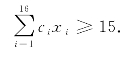
5m长的钢管至少10根，有

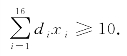
为实现最多使用3种切割模式

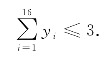
增设0～1变量yi，i=1，2，…，16.当yi=0时，xi=0，表示不使用第i种切割模式；当yi=1时，xi≥1，表示使用第i种切割模式.因此有：xi≥yi，xi≤Myi，i=1，2，…，16.其中M足够大，如这里取100.

因此模型为

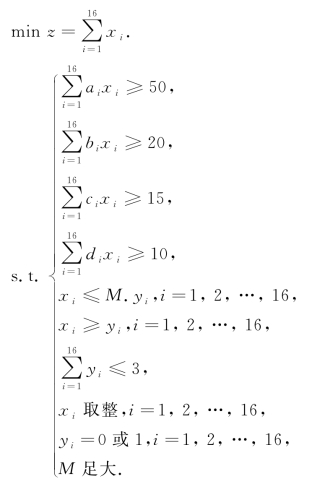
当所用钢管z最少时，求得的解为

x2=8,x13=10,x15=10.

目标值z=28.

即8根钢管采用切割模式2：2根8m，余料3m.

10根钢管采用切割模式13：2根4m，1根6m，1根5m，余料为0.

10根钢管采用切割模式15：3根4m，1根6m，余料1m.

切割模式采用了3种，余料为34，使用钢管z=28根.

LINGO程序为：

6.3.3.2 0～1规划模型

1.篮球对选队员问题

篮球队要选择5名队员上场组成出场阵容参加比赛.8名篮球队员的身高及擅长位置见表6-22.

表6-22 篮球队员数据

出场阵容满足如下条件：

（1）只能有一名中锋上场；

（2）至少有一名后卫上场；

（3）如1号和4号均上场，则6号不出场；

（4）2号和8号至少有1个不出场；(www.xing528.com)

问应当选择哪5名队员上场，才能使出场队员平均身高最高.

分析与求解

这是一个0～1整数规划问题.

设0～1变量xi如下

设各队员的身高分别用常数ai（i=1，2，…，8）来表示，则目标函数很容易给出

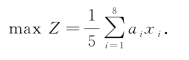
问题较为复杂的是如何根据题目给出的条件给出线性约束条件，下面对每一个条件给出约束条件：

所选队员为5人，则.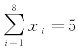

只能有一名中锋上场，则x1+x2=1，这样保证两名中锋恰好有一名上场.

至少有一名后卫，则x6+x7+x8≥1.

如1号和4号均上场，则6号不出场.则可用如下约束来表达：x1+x4+x6≤2.当x1=1，

x2=1时，则x6=0，满足条件；当x1=1，x2=0或x1=0，

x2=1,x6

可为0或1，也满足条件；当x1=0，

x2=0,

x6可为0或1，满足条件.因此用该约束条件完全可代表该条件.

2号和8号至少有1个不出场，即2号和8号至多出场1个.用约束条件来表达就是：x2+x8≤1.

因此对该问题建立的数学模型如下

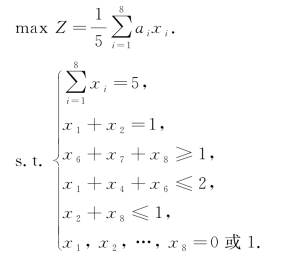
用LINGO编程如下：

所得到的解为：

x(1)=0,x(2)=1,x(3)=1,x(4)=1,x(5)=1,x(6)=1,x(7)=0,x(8)=0

即第2，3，4，5，6名队员被选上.

最大平均身高为Z=1.864m.

2.完成任务问题

有五项设计任务可供选择.各项设计任务的预期完成时间分别为3，8，5，4，10（周）设计报酬分别为7，17，11，9，21（万元）.设计任务只能一项一项地进行，总的期限为20周.选择任务时必须满足下面要求：

至少完成3项设计任务.若选择任务1，必须同时选择任务2.任务3和任务4不能同时选择.

应当选择哪些任务，才能使总的设计报酬最大？

分析与求解

这是一个0～1整数规划问题.

设0～1变量xi如下

设各项设计任务的完成时间为ti（i=1，2，…，5）表示，设计报酬为mi（i=1，2，…，5）表示.则容易得到目标函数

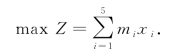
根据题目要求分别列出约束条件如下：

总期限为避免20周，则约束条件为

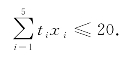
至少完成3项设计任务，则

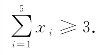
若选择任务1，必须同时选择任务2，则x2≥x1.

任务3和任务4不能同时选择，则x3+x4≤1，该约束表达式表明任务3和任务4至多只能选择1个.

因此对该问题建立的数学模型如下

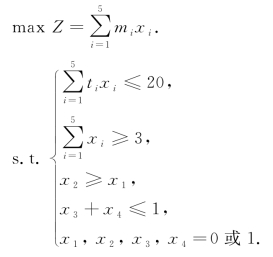
LINGO程序如下：

即在满足各种约束条件下，选择设计任务1，2，3，可使总报酬达到最大为35万元.

3.公交司机排班问题

某昼夜服务的公交路线每天各时间区段内需司机和乘务人员见表6-23.

设司机和乘务人员分别在各时间区段一开始上班，并连续工作8h，问该公交线路至少配备多少名司机和乘务人员？从第一班开始排，试建立线性模型.

表6-23 公交运行需求

模型分析与求解

注意 在每一时间段里上班的司机和乘务人员中，既包括在该时间段内开始时报到的人员，还包括在上一时间段工作的人员.因为每一时间段只有4h，而每个司乘人员却要连续工作8h.因此每班的人员应理解为该班次相应时间段开始时报到的人员.

设xi为第i班应报到的人员（i=1，2，…，6），则应配备人员总数为

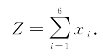
按所需人数最少的要求，可得到线性模型如下

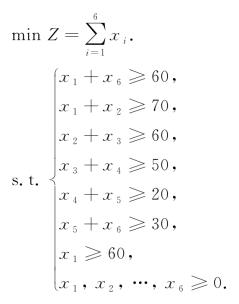
LINGO程序如下：

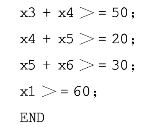
得到的解为：

配备的司机和乘务人员最少为150人.

课后提升

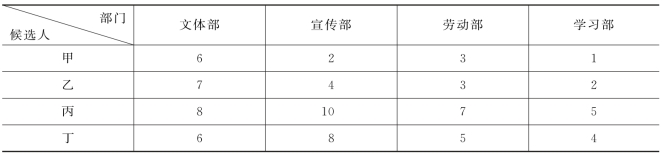
1.某校学生会准备在学生中选拔文体部、宣传部、劳动部、学习部四个部门的部长，经过层层筛选，最后剩甲、乙、丙、丁四名候选人，根据各项考核与民主测评，把四人主持各部的工作能力（量化为分值）列表见表6-24，试综合考虑四名候选人的情况，确定四个部长的最优选择方案.

线性规划发展简史

表6-24 候选人能力量化

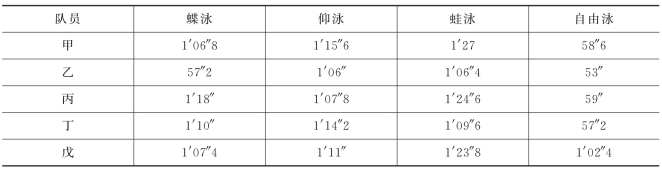
2.某班准备从5名游泳队员中选择4人组成接力队，参加学校的4×100m混合泳接力比赛.5名队员4种泳姿的百米成绩见表6-25.问：应该如何选拔队员组成接力队？

表6-25 游泳队员数据

答案

1.甲劳动部部长，乙文体部部长，丙宣传部部长，丁学习部部长.

2.甲参加自由泳，乙参加蝶泳，丙参加仰泳，丁参加蛙泳.