例1 求解下列二元一次线性方程组.
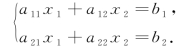
解 由消元法得
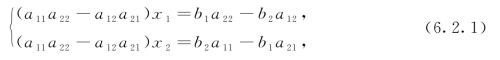
则
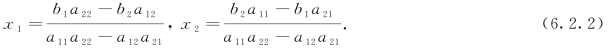
观察上面二元线性方程组式(6.2.1)解的一般形式(6.2.2)特点:两个未知数x1,x2的解有相同的分母,且分母只与方程组中未知数的系数有关.把这些系数按其在原方程组中的位置写出,记为
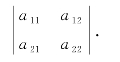
以此表示代数和(相同的分母)a11a22-a12a21,记作D,即
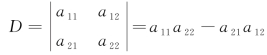 ,称作二阶行列式.
,称作二阶行列式.
由此得到行列式的概念.
定义1 把由2×2=4个数构成的2行2列的代数式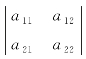 称为二阶行列式,记作D=a11a22-a21a12.其中,aij称为行列式的元素;横排称为行;竖排称为列;aij中下标的第一个数字表示这个元素所在的行数,下标的第二个数字表示这个元素所在的列数.
称为二阶行列式,记作D=a11a22-a21a12.其中,aij称为行列式的元素;横排称为行;竖排称为列;aij中下标的第一个数字表示这个元素所在的行数,下标的第二个数字表示这个元素所在的列数.
如图6-5所示,行列式中从左上角到右下角的对角线叫做主对角线,从左下角到右上角的对角线叫做副对角线.
对角线法则:二阶行列式的值等于主对角线上的两个元素的乘积减去副对角线上的两个元素的乘积.
同理,二元线性方程组(1)的两个未知数x1,x2的解中对应的分子分别记为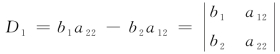 ,
,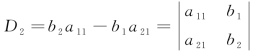 .
.
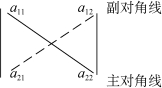
图6-5 二阶行列式对角线法则图
则,二元线性方程组的解为
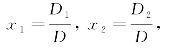
例2 求解二元线性方程组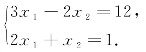
解 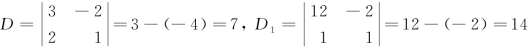 ,
,![]() ,
,
因此,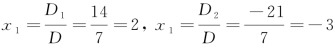 .
.
定义2 类似于二阶行列式,我们可以从三元一次线性方程组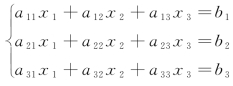 的求解中引入三阶行列式的概念.由32=9个元素排成的3行3列的代数式
的求解中引入三阶行列式的概念.由32=9个元素排成的3行3列的代数式 称为三阶行列式.
称为三阶行列式.
可根据对角线法则来记忆此行列式的值.
如图6-6所示,三条实线上的元素的乘积分别取正号,三条虚线上的元素的乘积分别取负号.
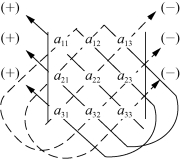
图6-6 三阶行列式对角线法则图
三阶行列式也可以用二阶行列式来计算,即

同理
D1=b1a22a33+a12a23b3+a13b2a32-b1a23a32-a12b2a33-a13a22b3,
D2=a11b2a33+b1a23a31+a13a21b3-a11a23b1-b1a21a33-a13b2a31,
D3=a11b3a22+b2a12a31+b1a21a32-a11b2a32-a12a21b3-b1a22a31,
则
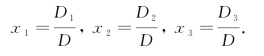
例3 计算三阶行列式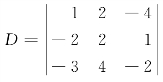 .
.
解法一 按对角线法则,有
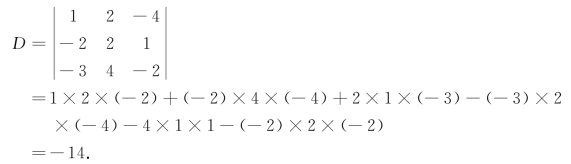
解法二(https://www.xing528.com)
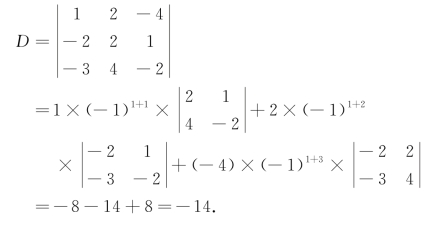
在MATLAB的Command Window窗口输入

定义3
由n2个元素排成的n行n列的符号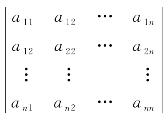 称为n阶行列式,通常记为Dn.其中aij(1≤i,j≤n)称为Dn的元素.Dn的值规定如下
称为n阶行列式,通常记为Dn.其中aij(1≤i,j≤n)称为Dn的元素.Dn的值规定如下
Dn=ai1Ai1+ai2Ai2+…+ainAin(i=1,2,…,n),
或
Dn=a1jA1j+a2jA2j+…+anjAnj(j=1,2,…,n),
上述行列式的定义又称为行列式按某一行或某一列展开.
其中Aij=(-1)i+j(i,j=1,2,…,n),Aij称为元素aij的代数余子式.Mij称为元素aij的余子式,其中余子式Mij是由行列式Dn去掉第i行和第j列元素后剩下的n-1阶行列式,即
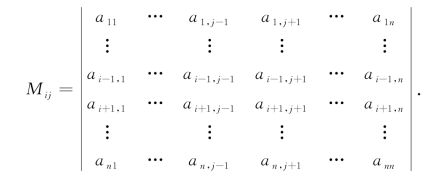
行列式按某一行或某一列展开后,理论上可以计算出任何行列式的值.
例4 计算四阶行列式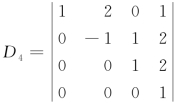 .
.
解
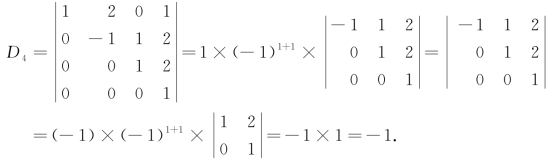
注意 如果行列式Dn中有某一行(列)元素含有较多的0,则按照那一行(列)去计算行列式的值比较容易.
在MATLAB的Command Window窗口输入

例5 求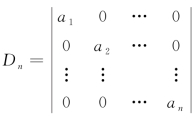 的值.
的值.
解
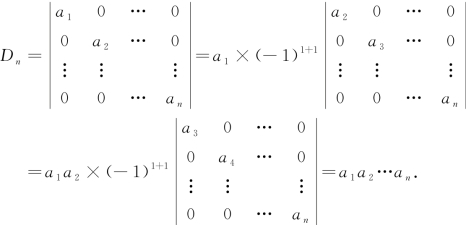
上述行列式称为对角形行列式,其特点是:除了主对角线之外的元素都为零.此行列式的值等于主对角线元素的乘积.
例6 求 的值.
的值.
解 把Dn按第一行展开有
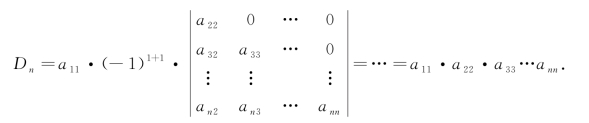
上述行列式,其主对角线上方的元素都为零.这样的行列式称为下三角形行列式,此行列式的值等于主对角线上元素的乘积.
还有一种类型的行列式,称为上三角形行列式.其特点是:主对角线下方的元素都为零.此行列式的值等于主对角线上元素的乘积.
课后提升
1.简述行列式与矩阵的定义,比较二者的异同点.
2.求下列行列式的值.

3.用行列式解下列方程组.

答案
1.略.
2.(1)16;(2)-77.
3.(1)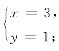 (2)
(2)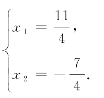
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




