如何使用逆矩阵解线性方程组

6.1.4学习了用简化阶梯形矩阵解线性方程组，6.1.5学习了用矩阵的秩判断线性方程组解的情况.下面，我们来学习用逆矩阵解线性方程组.

在式（6.1.2）中，m×n线性方程组

系数矩阵

未知数矩阵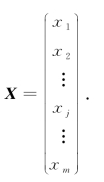

常数项矩阵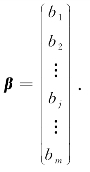

上边的线性方程组用矩阵可表示为AX=β，

等式两端边的左边同乘以A-1得，A-1AX=A-1β.

因为A-1A=E，

所以EX=A-1β.

又因为EX=X，

所以，X=A-1β.

由上面的推理可知，线性方程组用逆矩阵解线性方程组的步骤是：

（1）分别写出线性方程组系数矩阵A，未知数矩阵X和常数项矩阵β；

（2）求系数矩阵A的逆矩阵A-1；

（3）用矩阵的乘法运算求得A-1β得X.

例1 用逆矩阵求解线性方程组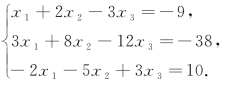

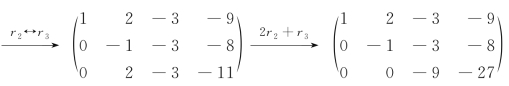线性方程组R（A）=R（B）=3，未知数的个数是3，所以，线性方程组有唯一解.(www.xing528.com)

线性方程组的系数矩阵，未知数矩阵和常数项矩阵分别是

所以，X=A-1β.

所以，原方程组的解为

有上面解的过程可以看出，用逆矩阵解线性方程组比较麻烦，而且只有方阵才可能有逆矩阵，所以该方法解线性方程组有一定的局限性，系数矩阵必须是方阵.用简化阶梯形矩阵或阶梯形矩阵解线性方程组相对要简便很多，而且系数矩阵不受方阵的限制，它使用于解各种情况的线性方程组.

使用MATLAB程序，用逆矩阵解线性方程组会非常简便.程序如下：

定义 对于式（6.1.2）的线性方程组，若右端常数项全为零，则称为齐次线性方程组.它的系数矩阵A与增广矩阵B的秩总是相等的，即R（A）=R（B），所以齐次线性方程组总是有解的，并由定理1知道：

（1）当R（A）=n时，齐次方程组有唯一的一组零解（x1=0，x2=0，…，xn=0）；

（2）当R（A）＜n时，齐次线性方程组有无穷多组解，易知齐次线性方程组有非零解的充要条件是R（A）＜n.

例4 求解齐次线性方程组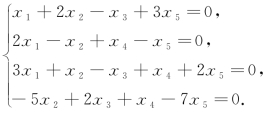

解

由于R（A）=2＜n=5，故有非零解，原方程组同解方程组为

令

x3=c1,x4=c2,x5=c3.

故得非零解