在这一节内容中,我们来学习矩阵的加减法,矩阵的数乘,矩阵的乘法,矩阵的转置等运算.它们在线性代数所讨论的一些问题中有着广泛的应用.
定义1 若两个矩阵A和B具有相同的行数与列数,则称矩阵A和B为同型矩阵;若它们的对应位置元素相等,则称矩阵A和B为相等矩阵,记作A= B.
定义2 设同型矩阵A=(aij)m×n,B=(bij)m×n,矩阵A和B的和记为A+B,规定
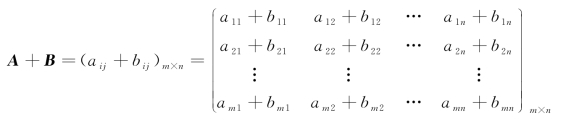
即,A+B等于矩阵A与矩阵B对应位置上的元素相加.
例1 设![]() ,求A+ B.
,求A+ B.
解 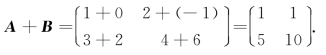
用MATLAB软件求矩阵加法的程序如下:
在MATLAB的Command Window窗口输入

矩阵加法有如下性质:设A,B,C是3个同型矩阵,则
(1)交换律A+B=B+A;
(2)结合律(A+B)+C=A+(B+C);
(3)A+O=O+A=A,其中,O是与A同型的零矩阵.
定义3 设同型矩阵A=(aij)m×n,B=(bij)m×n,矩阵A和B的差记为A-B,规定
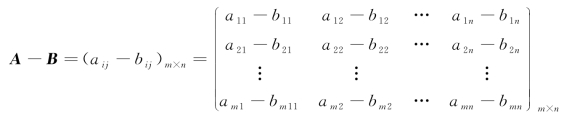
即,A-B矩阵A与矩阵B对应位置上的元素相减.
例2 设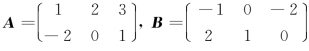 ,求A- B.
,求A- B.
解 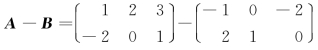
![]()
用MATLAB软件求矩阵减法的程序如下:
在MATLAB的Command Window窗口输入

定义4 以实数k乘以矩阵A中的每一个元素后得到的矩阵,称为数k与矩阵A的乘积,简称数乘矩阵.记作kA.即若A=(aij)m×n,则

即,kA就是用k乘以矩阵A中的每个元素.
矩阵的数乘运算满足以下性质:设A,B是2个同型矩阵,k,l是两个为常数,则
(1)1×A=A,0×A=O,k×O=O,其中,O是与A同型的零矩阵;
(2)k(lA)=l(kA)=(kl)A;
(3)k(A+B)=kA+kB;
(4)(k+l)A=kA+lA.
例3 设![]() ,求3A.
,求3A.
解 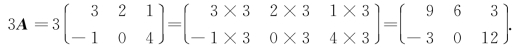
用MATLAB软件求数乘矩阵的程序如下:
在MATLAB的Command Window窗口输入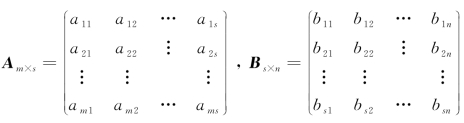

定义5 设,则规定矩阵A与B的乘积为矩阵C=(cij)m×n,其中,cij为矩阵A的第i行每个元素分别与矩阵B的第j列每个对应元素的乘积之和.即
![]()
由此可见,只有当矩阵A的列数与矩阵B的行数相同时,矩阵A与B才能进行乘法运算;矩阵C的行数与矩阵Am×s的行数相同,矩阵C的列数与矩阵Bs×n的列数相同.即取左矩阵的行数,右矩阵的列数作为矩阵C的行数和列数.

数与矩阵计算的异同
例4 设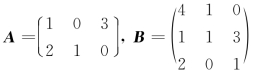 ,求A B.
,求A B.
解
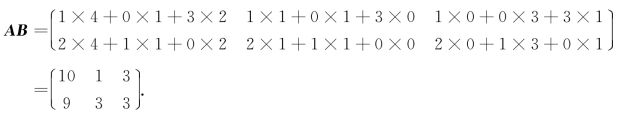
用MATLAB软件求矩阵乘积的程序如下:
在MATLAB的Command Window窗口输入

例5 设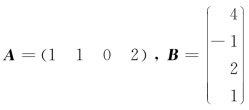 ,求AB,BA.
,求AB,BA.
解
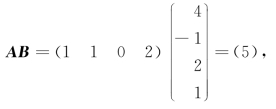
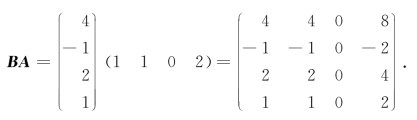
此题说明AB≠BA.
例6 设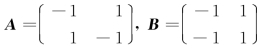 ,求AB,BA.
,求AB,BA.
解
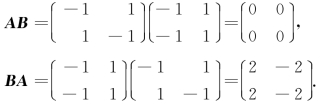
此题说明非零矩阵相乘可以是零矩阵,AB≠BA.
例7 设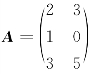 ,求AE和EA.
,求AE和EA.
解 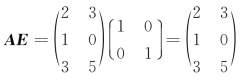 ,
,
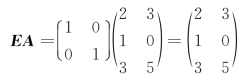 .
.
此题说明EA=AE.
注意
(1)由以上计算可知,即使矩阵A与B为同型矩阵,AB也不一定等于BA,即矩阵乘法不满足交换律;
(2)若矩阵AB=O,则不一定有A=O或B=O.即若矩阵AB=AC,不一定有B=C;
(3)矩阵乘法不满足消去律.AC=BC,不能消去C而推得A=B;
(4)两个非零矩阵的乘积可能是零矩阵(如例6);
(5)矩阵A与和它同阶的单位矩阵E的乘积AE=EA(如例7).
定义6
矩阵 是
是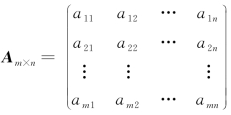 的转置矩阵,记作AT.
的转置矩阵,记作AT.
如,矩阵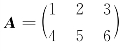 ,则
,则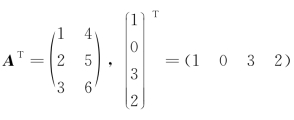 .
.
转置矩阵有如下性质:
(1)(AT)T=A;
(2)(A+B)T=AT+BT;
(3)(kA)T=kAT;
(4)(AB)T=BTAT.
定义7 A为n阶方阵,若存在同阶方阵B,使得AB=BA=E,则称矩阵A为可逆矩阵,矩阵B称为矩阵A的逆矩阵,记为B=A-1.
由上面的定义可知,不是所有的矩阵都存在逆矩阵.如果A不存在逆矩阵,则A称为不可逆矩阵.
可逆矩阵具有以下性质:
(1)若矩阵A可逆,则矩阵A-1是唯一存在的;
(2)若矩阵A可逆,k≠0,则矩阵kA也可逆,且![]() ;
;
(3)若矩阵A可逆,则矩阵A-1也可逆,且(A-1)-1=A;
(4)若矩阵A可逆,则矩阵AT也可逆,且(AT)-1=(A-1)T;
(5)若矩阵A和B为同阶可逆矩阵,则AB也可逆,且(AB)-1=B-1A-1.(https://www.xing528.com)
下面介绍利用初等行变换求逆矩阵的方法.
具体步骤是:
(1)把方阵A和A的同阶单位矩阵E写成一个n×2n矩阵(A︙E);
(2)对矩阵(A︙E)进行初等行变换,使虚线的左侧A化成单位矩阵E,虚线右侧E变成A-1,即![]() .
.
例8 求矩阵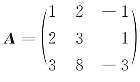 的逆矩阵.
的逆矩阵.
解
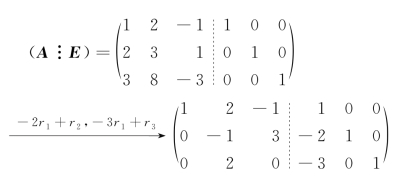

所以,A的逆矩阵为
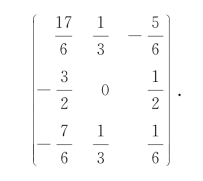
用MATLAB软件求逆矩阵的程序如下:
在MATLAB的Command Window窗口输入

例9 求矩阵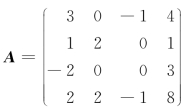 的逆矩阵.
的逆矩阵.
解 

上边最后的矩阵中虚线左侧出现零行,所以A矩阵是不可逆的.
用初等行变换求逆矩阵,把判断矩阵是否可逆与求逆矩阵一次完成,不必先判断矩阵是否可逆.
在MATLAB的Command Window窗口输入出现下列情况.

例10 已知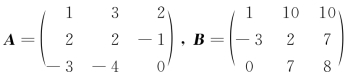 ,解矩阵方程AX= B.
,解矩阵方程AX= B.
解 因为AX=B,
所以A-1AX=A-1B,
EX=A-1B,
X=A-1B,
为了求未知矩阵X,可先求A-1,再做矩阵的乘法运算A-1 B.
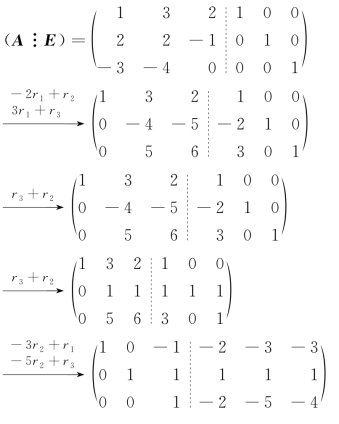
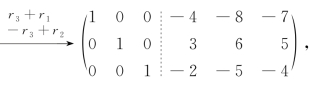
所以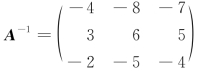 ,
,
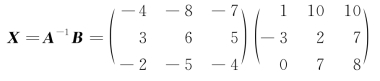
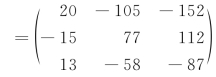 .
.
用MATLAB软件求未知矩阵X的程序如下:
在MATLAB的Command Window窗口输入

课后提升
1.设矩阵.
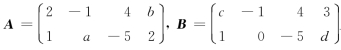 且A=B,求元素a,b,c,d的数值.
且A=B,求元素a,b,c,d的数值.
2.设矩阵.
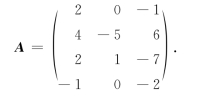
求-A.
3.已知.
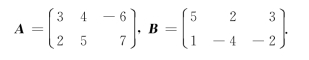
求(1)A+B;(2)![]() ;(3)3A- B.
;(3)3A- B.
4.已知.
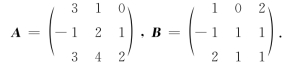
求满足方程3A-X=B中的X.
5.计算下列矩阵乘积.
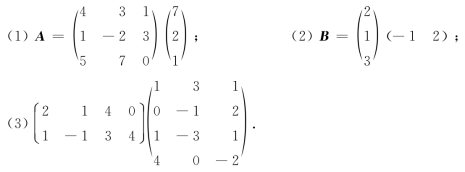
6.已知:
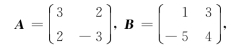
求AB-BA.
7.将下面各题用矩阵表示,并且用矩阵的运算求出各题的结果.
(1)某厂一、二、三车间都生产甲、乙两种产品,上半年和下半年的产量(t)见表6-10.
表6-10 两种产品的产量 单位:t

求①三个车间全年的产量分别是多少?
②各车间下半年比上半年多生产多少吨?
(2)某校明后两年计划建造教学楼和宿舍楼,建筑面积及材料耗用量见表6-11.
表6-11 建筑面积及材料用量

求明后两年三种建筑材料用量各为多少?
(3)某集团公司的四个生产基地均能生产甲、乙、丙三种产品,其单位成本(元/件)见表6-12.
表6-12 产品的生产成本 单位:元/件
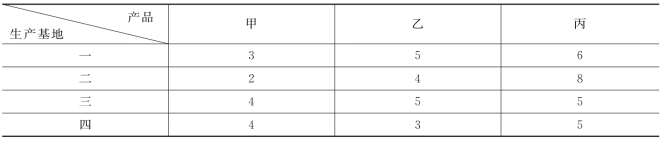
现要求生产甲种产品600件,乙种产品50件,丙种产品200件,问哪个工厂的生产成本最低?
(4)某厂生产五种产品,1~3月份生产产量及产品的单位价格见表6-13.
表6-13 产品的单价及产量 单位:万元
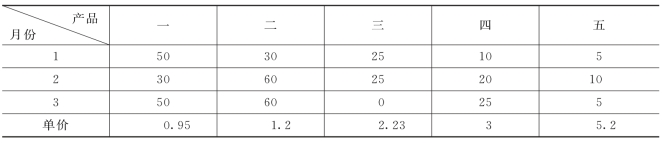
求该厂每个月的总产值是多少?
答案
1.略.
2.略.
3.(1)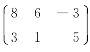 ;(2)
;(2)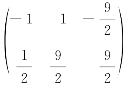 ;(3)
;(3)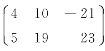 .
.
4.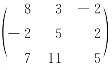 .
.
5.(1)![]() ;(2)
;(2)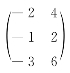 ;(3)
;(3)![]() .
.
6.![]() .
.
7.(1)① .
.
②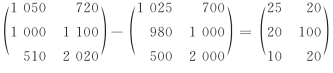 ;
;
(2)![]() ;
;
(3)第二个生产基地的成本最低;
(4) .
.
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




