高职数学下册：简化阶梯形矩阵解线性方程组

在6.1.2中，我们学习了线性方程组的初等变换，下面来学习矩阵的初等行变换，它与线性方程组的初等变换相类似.

定义1

下面的三种变换统称称为矩阵的初等行变换：

（1）对调两行（对调i，j两行，记作ri↔rj）；

（2）用数k≠0乘以某一行中的所有元素（k乘第i行，记作kri）；

（3）把某一行所有元素的k倍加到另一行对应元素上（第i行的k倍加到第j行上，记作kri+rj），第i行不变，第j行改变.

定理

任意矩阵都可以经过有限次的初等行变换化为简化阶梯形矩阵.

求矩阵A的简化阶梯形矩阵的步骤为：

（1）用矩阵的初等行变换把A化为阶梯形矩阵B；

（2）用矩阵的初等行变换把阶梯形矩阵B中非零行的第一个非零元素全部化为1（主元），得到阶梯形矩阵C；

（3）用矩阵的初等行变换，从下往上，依次把阶梯形矩阵C中主元所在列的其他元素都化为零，得到简化阶梯形矩阵 D.

例1 把矩阵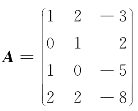化为简化阶梯形矩阵.

解

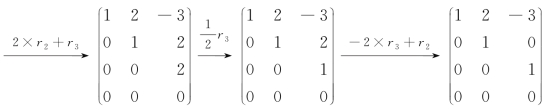
用MATLAB软件求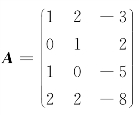的简化阶梯形矩阵程序如下：

在MATLAB的Command Window窗口输入

注意 矩阵的初等行变换每一步都要用箭头“→”标出，而不是等号.

线性方程组可以用增广矩阵表示，对增广矩阵进行初等行变换化为简化阶梯形矩阵，简化阶梯形矩阵又可以返回到方程组的形式.下面我们用简化阶梯形矩阵解线性方程组.

用简化阶梯形矩阵解线性方程组的步骤是：

（1）写出线性方程组的增广矩阵B；(www.xing528.com)

（2）求出增广矩阵B的简化阶梯形矩阵；

（3）写出简化阶梯形矩阵对应的线性方程组.

例2 用简化阶梯形矩阵解下列线性方程组.

解

（1）设线性方程组的增广矩阵为B

增广矩阵的简化阶梯形矩阵对应的线性方程组为

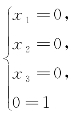显然，第四个方程0=1是不成立的.所以，该方程组无解.

（2）设线性方程组的增广矩阵为B

增广矩阵的简化阶梯形矩阵对应的线性方程组的解为

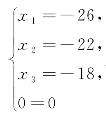显然，该方程组的解是唯一的.

（3）设线性方程组的增广矩阵为B

增广矩阵的简化阶梯形矩阵对应的线性方程组为

所以方程组有无穷多解，x3为自由变量.

例2中用MATLAB软件求增广矩阵B的简化阶梯形矩阵，更为简便.程序为

例2可以看出，将方程组转化成增广矩阵，用初等行变换，把增广矩阵化为简化阶梯形矩阵，从而达到解线性方程组的目的.这实际上与线性方程组的加减消元法是一致的.对增广矩阵施以初等行变换，相当于把原方程组变化成一个新的同解方程组.区别是，用矩阵解线性方程组，在书写上省去了未知数，只有未知数的系数和常数项参与运算过程.使用MATLAB软件求线性方程组增广矩阵的简化阶梯形矩阵，会使线性方程组的求解更为简便.

课后提升

1.求下列矩阵的简化阶梯形矩阵.

2.用简化阶梯形矩阵求下列方程.

答案