消元法解线性方程组的应用

下面，我们来解决6.1.1中最后所提出的问题.

我们把中学学习的用加减消元法解方程组的方法推广到解n元线性方程组中.

定义1

设

与

以上两个方程组都是以x1，x2，…，xn为未知数的线性方程组，如果方程组（6.1.3）的解都是方程组（6.1.4）的解，方程组（6.1.4）的解也都是方程组（6.1.3）的解，那么，这两个方程组称为同解方程组.

一般地，一个线性方程组可以经过下列三种变换：

（1）互换两个方程的位置.如第i个方程和第j个方程互换位置；

（2）方程组中的一个方程乘以非零常数k.如第i个方程两边同乘以非零常数k；

（3）一个方程的k倍加到另一个方程上.如第i个方程的k倍加到第j个方程上，第i个方程不变，第j个方程改变.

以上三种变换统称为线性方程组的初等变换.

例1

①与③互换位置，得新方程组（6.1.6）为

在方程组（6.1.6）中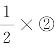，得新方程组（6.1.7）为

在方程组（6.1.7）中（-2）×①+③，得新方程组（6.1.8）为

以上方程组（6.1.5），（6.1.6），（6.1.7），（6.1.8）都是同解方程组.

定理1 如果一个线性方程组经过有限次的初等变换后，得到新的方程组，则新方程组与原方程组为同解方程组.

利用前面所学到的线性方程组的初等变换和同解方程组的知识来解线性方程组.

例2 求下列线性方程组的解.

解

去掉方程0=0，得

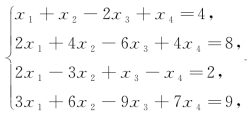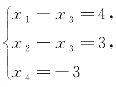与方程组是同解.(www.xing528.com)

所以，原方程组

将方程组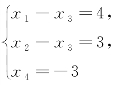中的未知数x3移到等号右端，得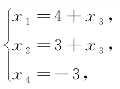

令x3=C（C为任意常数），可得原方程组的解为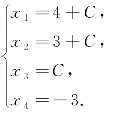

例2解方程组过程中，后几步用的是代入法消去未知数，前几步用的是加减法消去未知数，通常称为加减消元法和代入消元法.

定义2

加减消元法是指利用方程组的初等变换，使方程组中的某一个未知数的系数的绝对值相等，然后把两个方程相加或相减，以消去这个未知数，从而使方程中未知数的个数减少，得以求解.

代入消元法是将方程组中的一个方程的未知数用含有其他未知数的代数式表示，并代入到另一个方程中去，这样就消去了一个未知数，从而使方程中未知数的个数减少，得以求解.

定义3

例2中，方程组有无穷多解，此种表达式为方程组的所有解，称为方程组的通解，其中x3为自由项.

上例的解方程组很复杂，我们尝试去寻找更为简便的方法.观察例题的解方程组过程，我们得到如下结论：

（1）所有的运算只出现在相同未知数的系数之间和常数之间，而未知数没有参与运算；

（2）线性方程组

与有序数组一一对应

由以上的结论，我们引出矩阵的定义.用矩阵解线性方程组更为简便.

课后提升

1.方程组A经过初等变换后得到方程组B，则A与B的解是否相同？

2.用消元法解下列方程组.

答案

1.相同.