解n元线性方程组，高职应用数学(下)

在平面解析几何中，两条直线的位置关系从几何角度考虑，有平行、相交、重合三种，相应地，两条直线的交点有下列三种情况：无交点，一个交点和无数个交点.两条直线的位置关系从代数角度考虑，利用两条直线方程构成的方程组，对方程组求解，也对应有下列三种情况：无解，一组解和无数组解.

引例1

（1）直线2x+y=5和直线2x+y=1平行，无交点，

即方程组无解.

（2）直线2x+y=3和直线2x-y=5相交，且有一个交点（2，-1），

即方程组的解为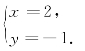

（3）直线2x+y=1和直线6x+3y=3重合，有无数个交点，

即方程组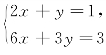有无数组解.

以上每个方程都是含有两个未知数，且未知数的次数都是1次，统称为二元一次方程.二元一次方程构成的方程组称为二元一次方程组.

引例2

中的每一个方程都是含有三个未知数，且未知数的次数都是1次的三元一次方程.三元一次方程构成的方程组称为三元一次方程组.

引例3

同样地，是四元一次方程构成的方程组，称之为四元一次方程组.

我们把上面的二元一次方程，三元一次方程，二元一次方程组，三元一次方程组，四元一次方程组做进一步的推广，来学习n元线性方程和n元线性方程组.

定义1 设a1，a2，…，aj，…，an，b1都是常数，x1，x2，…，xj，…，xn是未知数，则表达式称式（6.1.1）为n元线性方程.其中常数aj是未知数xj的系数，j=1，2，3，…，n，b1是常数项.

定义2 对于n元线性方程式（6.1.1）a1x1+a2x2+…+ajxj+…+anxn=b1

如果存在n个常数c1，c2，…，cj，…，cn，且a1c1+a2c2+…+ajcj+…+ancn=b1，显然，x1=c1，x2=c2，…，xj=cj，…，xn=cn.

则称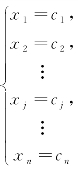是线性方程式（6.1.1）的一个解.

定义3 由m个n元线性方程构成的方程组

称式（6.1.2）为n元线性方程组.其中aij（i=1，2，3，…，m，j=1，2，3，…，n）表示方程组（6.1.2）中未知数xj的系数；aij中的i是方程组中第i个方程的标号，aij中的j是方程中第j个未知数的标号；bi中的i是方程组中第i个方程的标号.

定义4 如果存在n个常数c1，c2，…，cj，…，cn，使得是线性方程组（6.1.2）中所有方程的解，则称是线性方程组（6.1.2）的一个解.

例1 判断下列未知数的值是否为方程组的解.

(1)x=1,y=4,z=9;(2)x1=1,y=2,z=3;(3)x=-41,y=29,z=0.

解 （1）把x=1，y=4，z=9代入方程组等号左边，得

显然，x=1，y=4，z=9不满足第二方程和第三个方程.

所以，x=1，y=4，z=9不是方程组的解.

（2）把x=1，y=2，z=3，代入方程组等号左边，得

显然，x=1，y=2，z=3满足三个方程.

所以，x=1，y=2，z=3是方程组的解.

（3）把x=-41，y=29，z=0代入方程组等号左边，得(www.xing528.com)

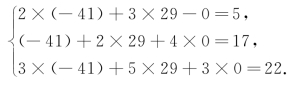
显然，x=-41，y=29，z=0满足三个方程.所以x=-41，y=29，z=0是方程组的解.

从例题中，我们可以看出x=1，y=2，z=3和x=-41，y=29，z=0都是这个程组的解，所以该方程组的解不是唯一的.

例2 求下列方程组的解.

(1) (2) (3)

解 采用中学学习的加减消元法，来解方程组.

(1)

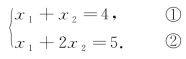
②-①得x2=1

把x2=1带入①得x1=3

所以方程组的解为

(2)

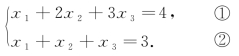
①-②得x2+2x3=1，一个方程中有两个未知数，当x3取不同的常数时，x2就有对应的数值.不妨取x3=0，

x3=1,x3=2,

x3=-1，…，则x2=1，x2=-1，x2=-3，x2=3，….

把x2，x3对应的值带入到②中，得到方程组的解为…

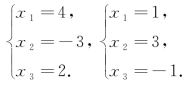(3)

②-①得x1+2x2=1，它与①相矛盾，所以该方程组无解.

从例2中，可以看到方程组（1）有一组解，方程组（2）有无数组解，方程组（3）无解.

一般地，一个线性方程组可能无解，也可能有解.有解时，它的解可能有无数组，也可能只有一组.

那么，如何判断一个线性方程组是否有解？有解时，如何判断其解是无数组还是只有一组？如何求出它的解？

课后提升

1.求下列线性方程组的解.

(1)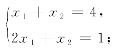 (2) (3)

2.当前，中国农村发展进入新阶段，家庭农场越来越受到人们的喜爱.小明到一个农场度假，他看到草地上有一群鸡和羊.他数了一下，共有23个头和64条腿.草地上分别有多少只鸡和羊？

3.某商场用36万元购进A，B两种商品，销售完后共获利6万元，其进价和售价见表6-6.

表6-6 商品进售价 单位：元/件

求该商场购进A，B两种商品各多少件？

答案

1.（1） （2）无解；（3）无数组解.

2.鸡14只，羊9只.

3.A商品200件，B商品120件.