高职应用数学：矩阵与线性方程组

在人们的社会实践中，许多变量之间的关系可以直接或近似地表示成线性关系，可以表示成线性方程组.因此研究变量间的线性关系，解线性方程组是非常重要的.本节我们以中学阶段二元一次方程组的知识为学习起点，引出n元线性方程组的概念，学习把n元线性方程组写成矩阵的形式，用矩阵的秩判断线性方程组解的情况，用简化阶梯形矩阵、逆矩阵来解线性方程组.

案例1 当电流经过电阻（如电机或灯泡）时，会产生“电压降”.根据欧姆定律U=IR，其中U为电阻两端的“电压降”，I为流经电阻的电流强度，R为电阻，U，I和R的单位分别为福特、安培和欧姆.对于电路网络，任何一个闭合回路的电流服从希尔霍夫电压定律：沿某个方向环绕回路一周的所有电压降U的代数和等于沿同一方向环绕该回路一周的电源电压.求出图6-1中电流强度I1，I2，I3，I4的大小.

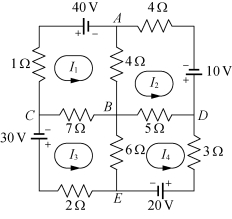
图6-1 电路

分析 电路图的4个回路中，每个电阻电压降的代数和等于电源电压，可列出方程组，解方程组可得到电流I1，I2，I3，I4的大小.

解 回路1中，各电阻的电压降总和为

I1+7I1+4I1-4I2-7I3=12I1-4I2-7I3.

回路2中，各电阻的电压降总和为

5I2+4I2+4I2-5I4-4I1=-4I1+13I2-5I4.

回路3中，各电阻的电压降总和为

2I3+6I3+7I3-7I1-6I4=-7I1+15I3-6I4.

回路4中，各电阻的电压降总和为

3I4+5I4+6I4-5I2-6I3=-5I2-6I3+14I4.

根据各回路上电压降总和等于电源电压，得到下列方程组为

在MATLAB命令窗口输入以下命令

所以，I1，I2，I3，I4的大小分别为13.16，8.51，11.98，9.61.

案例2 某城市的交通图如图6-2所示，每一条道路都是单行道，图中数字表示某一个时段的机动车流量.假设针对每一个十字路口，进入和离开的车辆数相等.计算每两个相邻十字路口间路段上的交通流量xi（i=1，2，3，4）.

图6-2 交通图

分析 根据交通图中的4个十字路口，进入和离开的车辆数相等，可列出4个方程构成的方程组，解方程组得到每两个相邻十字路口间路段上的交通流量x1，x2，x3，x4.

解 根据已知条件，得到十字路口的流通方程如下

A：x1+360=x2+260.

B：x2+220=x3+292.

C：x3+320=x4+357.

D：x4+260=x1+251.

整理以上方程得出方程组为

用初等行变换将方程组的增广矩阵化为简化阶梯形，

由于（A，β）的最后一行全为零，方程组中只有三个有效方程，所以有无穷组解，以x4为自由变量，其解为

令x4=c，得方程组得解为

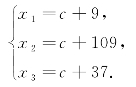
在MATLAB命令窗口输入以下命令

所以，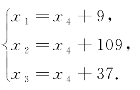

案例3 如图6-3所示的双杆系统中，杆1的重量G1=200N，长度L1=2m，水平方向的夹角，杆2重量G2=100N，长度m，与水平方向的夹角，三个铰接点A，B，C所在平面垂直于水平面.求杆1，杆2在铰接点处所受到的力.

图6-3 双杆系统

分析 在图6-3所示的双杆系统中，已知杆1重G1 =200N，长L1=2m，与水平方向的夹角为，杆2重G2=100N，长m，与水平方向的夹角为，三个铰接点A，B，C所在平面垂直与水平面.求杆1，杆2在铰接点处所受到的力.

假设两杆都是均匀的，在铰接点处的受力情况如图6-4所示.

对于杆1

水平方向受到的合力为零即N1-N3=0，故N1=N3.

竖直方向受到的合力为零即N2+N4-G1=0，故N2+N4=G1.

以点A为支点的合力矩为零即0，故

图6-4 两杆受力图解(www.xing528.com)

对于杆2，类似地有

此外还有N3=N7，N4=N8.于是将上述8个等式联立起来得到关于N1，N2，…，N8的线性方程组

在MATLAB命令窗口输入以下命令

案例4 现有木工、电工、油漆工各一人，他们相互装修每家的房子，工作的天数见表6-1.

表6-1 工作的天数 单位：d

他们签订协议如下：（1）每人工作10d（包括在自己家的日子）；（2）每人的日工资在60～80元之间；（3）日工资数应使每人的总收入和总支出相等.求每人的日工资.

分析 事实上各人都不必付自己工资，各家应付工资和各人应得收入见表6-2，这时各家应付工资和各人应得收入相等.x，y，z分别是木工，电工，油漆工的日工资.

表6-2 各家应付工资和各人应得收入 单位：元

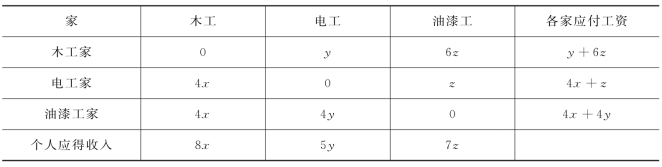
解 设木工，电工，油漆工的日工资分别是x，y，z，各人都不必付自己工资，则各家应付工资和各人应得收入相等.由此可得

在MATLAB命令窗口输入以下命令

上述齐次线性方程组的同解为

根据题中的第二个条件“每人日工资在60～80元之间”，得到

所以，木工、电工、油漆工的日工资分别为元，元，k元.

案例5 某公司生产A，B，C三种产品，每种产品的成本分为三类：原料成本、人工成本、管理与其他成本.每一类成本中，给出生产单位产品所需要的成本估计量，同时给出每季度生产每种产品的数量.以上数据见表6-3和表6-4.计算每季度生产三种产品的每类成本值.

表6-3 单位产品需要的成本 单位：元

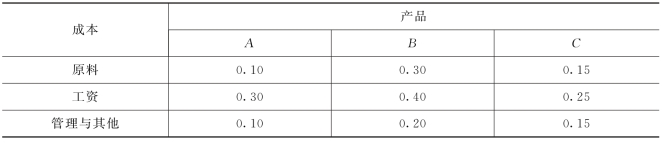
表6-4 每季度的产量 单位：件

分析

春季生产三种产品的原料成本值是：0.10×4000+0.30×2000+0.15×5800.

夏季生产三种产品的原料成本值是：0.10×4500+0.30×2600+0.15×6200.

秋季生产三种产品的原料成本值是：0.10×4500+0.30×2400+0.15×6000.

冬季生产三种产品的原料成本值是：0.10×4000+0.30×2200+0.15×6000.

春季生产三种产品的工资成本值是：0.30×4000+0.40×2000+0.25×5800.

夏季生产三种产品的工资成本值是：0.30×4500+0.40×2600+0.25×6200.

秋季生产三种产品的工资成本值是：0.30×4500+0.40×2400+0.25×6000.

冬季生产三种产品的工资成本值是：0.30×4000+0.40×2200+0.25×6000.

春季生产三种产品的管理与其他成本值是：0.10×4000+0.20×2000+0.15×5800.

夏季生产三种产品的管理与其他成本值是：0.10×4500+0.20×2600+0.15×6200.

秋季生产三种产品的管理与其他成本值是：0.10×4500+0.20×2400+0.15×6000.

冬季生产三种产品的管理与其他成本值是：0.10×4000+0.20×2200+0.15×6000.

实际上，每季度生产三种产品的每类成本值就是将表6-3中三种产品的三类成本分别与表6-4中每季度的产量对应数字相乘再相加.所以，用到矩阵乘法运算的知识.

解 表6-3对应的矩阵为，

表6-4对应的矩阵为，

.

在MATLAB命令窗口输入以下命令

每季度生产三种产品的每类成本值见表6-5.

表6-5 每季度的每类成本 单位：元