1）德尔菲法：德尔菲法又称专家调查法，是一种采用通信方式分别将所需解决的问题单独发送到各个专家手中，征询意见后回收汇总全部专家的意见，并整理出综合意见[23]。随后将该综合意见和预测问题再分别反馈给专家，再次征询意见，各专家依据综合意见修改自己原有的意见，然后再汇总。这样多次反复，逐步取得比较一致的预测结果的一种决策方法。德尔菲法依据系统中的程序，采用匿名发表意见的方式，即专家之间不得互相讨论，不发生横向联系，只能与调查人员发生关系，通过多轮次调查专家对问卷所提问题的看法，经过反复征询、归纳、修改，最后汇总成专家基本一致的看法，作为预测的结果。这种方法具有广泛的代表性，较为可靠。
2）场景描述法：精心设计一组假设上的未来场景，不同的假设会出现不同的场景。决策者决定每个场景的样子，然后做出决策。
3）直觉法：直觉法基于人脑处理信息的能力，主要用于团队工作中。每个人在无压力或是无恐惧感的情况下，提出自己的想法和建议。
4）专家会议法：专家会议法代表某一专家的判断或是一组专家的一致意见。专家们相互讨论，相互启发，集思广益以弥补个人判断的缺陷，使分析更细致、周全、具体、有效。但是专家会议也存在一些缺点，有些专家可能会受环境、心理、权威、自尊心等影响，导致预测结果的有效性。
5）移动平均法：移动平均法就是使用最近n个数据值预测下一时期的数据值，数学表达式为
式中 Ft——下一期的预测值；
n——移动平均的时期个数；
At-1——前期实际值；
At-2，At-3和At-n——前两期、前三期直至前n期的实际值。
所谓移动，就是当时间序列获得一个新的观察数据值，将数据代入式（6-1），替换最旧的一个数，即可计算下一个观察值。若存在新观察值出现，则平均值需要移动。
在使用移动平均值的时候，需要选择n个数据值。在预测中，还有一个指标是必不可少的——预测精度。现实中，希望预测误差尽可能地做到最小。使用预测误差或预测误差二次方和来度量预测精度。对于移动平均法来说，不同的移动长度，精度也不相同，因此在选择n个数据个数时，需要选择误差最小的。
6）加权移动平均法：加权移动平均法就是在移动平均值的基础上对每个数据加上权重。其公式为
式中 w1——第t-1期实际值的权重；
w2——第t-2期实际值的权重；
wn——第t-n期实际值的权重；
n——预测的时期数；
At-1——为前期实际值；
At-2，At-3和At-n分别为前两期、前三期直至前n期的实际值。
特别需要注意的是，权重之和恒等于1，即w1+w2+…+wn=1。并且一般情况下，最近的、最新的数据的权重相对来说比较大，因此加权移动平均法和移动平均法一样需要预测精度，这里不再介绍。
7）指数平滑法：指数平滑法是生产预测中最为常用的一种，简单的全期平均需要使用过去的全部数据，而移动平均不需要考虑较远的数据，加权移动平均则给予近期数据太大的权重。指数平滑法吸收了全期平均和移动平均的优点，在使用过去数据的条件下，只是逐渐减弱其在整体中的影响程度，即随着数据的远离，赋予逐渐收敛为零的权值[24]。
指数平滑法的基本公式是
式中 St——时间t的平滑值；
Yt——时间t的实际值；
St-1——时间t-1的平滑值；
α——平滑常数，其取值范围为[0，1]。
将式（6-3）展开
记β=（1-α），0＜β＜1，则式（6-4）简化为
上述式（6-3）、式（6-4）和式（6-5）是等价的。记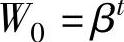
，W0为初始值S0的加权系数，记
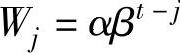，j=t，…，2，1；称Wj为Yj的加权系数，则(www.xing528.com)
当数据量较多时，初始值S0对指数平滑值St的影响相对较小，通常是直接用第1期的数据Y1作为初始值S0，但若数据量很少且平滑系数较小的情况下，则初始值S0对指数平滑值St将有着不可忽略的影响。可应用迭代方法（或全期指数加权平均法）直接计算St值[25]。
在指数平滑法中，另一个关键问题是如何选取平滑系数。在时序数据预测时
在式（6-6）中，新的预测值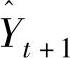
是根据本期的预测误差
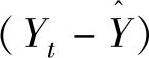对本期的预测值
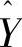调整后得到的。若时间序列存在较大的随机波动，则应选取较小的α，从而减小由随机波动所引起的预测误差值。若时间序列无较大随机波动，则选择较大的α，以实现快速收敛。
8）一元回归分析：一元回归分析模型为
y=ax+b（6-7）
a——估计回归方程截距；
b——估计回归方程的斜率；
x——自变量。
通常情况下，如果用一条直线近似表示数据的规律则可发现，虽然很接近，但是却有很多的点没有恰好落在直线上。但是仍需导出一个很接近的直线去表现这种关系，在数学上，通常采用最小二乘法推导回归方程式的方法来达到这一目的。最小二乘方法是现今最好的拟合方法。其思想是，估计数据与给定数据之间误差的二次方和为最小。
由最小二乘原理可以计算截距a和斜率b，其公式如下：
式（6-8）与式（6-9）中，n为观察个数，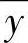
为因变量的平均值，
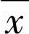为自变量的平均值。当b＞0时，x与y为正相关，当b＜0时，x与y为负相关。若将a，b代入，就可以建立出预测模型。
接下来，需要对x、y做相关系数分析，相关度公式为
相关系数r的特征有
•相关系数取值范围为：-1≤r≤1。
•r与b符合相同。当r＞0，称正线性相关，xi上升，yi呈线性增加。当r＜0，称负线性相关，xi上升，yi呈线性减少。
•|r|=0，X与Y无线性相关关系；|r|=1，完全确定的线性相关关系；0＜|r|＜1，X与Y存在一定的线性相关关系；其中，|r|＞0.7，为高度线性相关；0.3≤|r|≤0.7，为中度线性相关；0.3≤|r|，为低度线性相关。
9）一元线性回归预测法研究的是某一因变量与一个自变量之间的关系问题。但是，客观现象之间的联系是复杂的，许多现象的变动都涉及多个变量之间的数量关系。这种研究某一因变量与多个自变量之间的相互关系的理论和方法就是多元线性回归预测法。但是由于多元线性回归预测计算比较繁杂，故本节采用矩阵形式讨论多元线性回归预测法的基本原理。
•多元线性回归模型：设所研究的对象受多个因素x1，x2，…，xm影响，假定各个影响因素与y的关系是线性的，这时就需要建立多元线性回归模型。
其中yi，xi1，xi2…，xim为预测目标和影响因素的第i组观测值。若取x1的观测值恒等于1，即对任意i有xi1=1，则式（6-12）变为
其矩阵形式为
其中，
仍采用最小二乘法估计参数向量B，设观测值与模型估计值的残差向量为E，则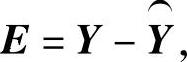
其中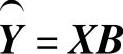
，根据最小二乘法的要求，应有
即
由极值原理，根据矩阵求导法则，上式对B求导，并令其等于零，则得
整理得回归系数向量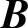
的估计值为
相关性公式为
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
