监测系统中的智能信息处理技术及其应用

最大似然估计是一种统计方法，它考虑由n个监测样本组成的集合D={x₁，x₂，…，x_n}。这些监测样本都是未标记的，并且是独立的从一个混合密度采样出来的。混合密度为

其中，参数向量θ具有确定但未知的值。样本集的似然函数具有下面的联合概率密度形式：

使得该密度达到最大的参数值θ就是θ的最大似然估计p（D|θ）。

如果p（D|θ）是关于θ的可微函数，就可以得出一些θ的必要条件。令l是似然函数的对数，▽_θ1l为l关于θ₁的梯度，那么

并且

假设参数向量θ_i和θ_j是互相独立的（i≠j），通过引入后验概率

可以发现对数似然的阶梯可写成如下形式

当l最大时，l在各个θ_t方向上的梯度为0，预示最大似然估计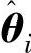必须满足

对这个方程求解，就可以得到最大似然估计。

不难将这些结果推广到把先验概率P（ω_i）也包含在未知量中。这时候，问题转化为寻找θ和P（ω_i）使得p（D|θ）取得最大值，并且要满足P（ω_i）≥0（i=1，…，c）和(www.xing528.com)

令表示的最大似然估计，为的最大似然估计。可以证明，如果似然函数是可微，并且对每个i都不为0，则

和必须满足下面的条件：

和

其中

根据该算法可以设计工业系统的评价标准和故障检测。参考文献^[11]用最大似然估计来诊断链路故障。300个模型节点在相同的网络环境下，设定不同的故障链路百分比或不同的时隙数，按照EM算法和联立方程组求解两种方法估计链路状态的先验概率。为了比较性能，先计算估计出的概率值同真实值的误差，然后绘制出误差累积量分布函数，即误差在各个范围内所占的比例。容易得出曲线上升的速度越快，对应算法的误差累积量越小（估计误差小的链路占的百分比多）。可见，用最大似然法估计链路的先验故障概率，以此来分析系统故障具有很好的效果。

参考文献^[12]将最大似然法应用到电网故障诊断及监测信号校正中。为了提高模型的容错性，提出了基于最大似然译码原理的监测信号信息校正方法，然后利用编码基本网在无畸变信号的基础上进行故障诊断。

诊断过程如下：首先对接收到的信息进行最大似然校正，得到传送信息的估值序列。根据估值序列中的断路器信息确定停电区域，最后利用停电范围内元件的基本网模型进行故障诊断。

利用最大似然译码原理对监测信号进行信息校正，然后通过编码基本网进行电网故障诊断的方法简单有效、容错性好、可移植性强，具有很好的应用前景。