输油系统奇异点获取结果

管道输送具有成本低，节省能源，安全性高及供给稳定等优点。它既能输送气体、液体，也能输送固体。因此，管输在工业、农业、国防等各行各业中得到广泛应用。以油气输送管道为例，目前全世界大型输油管道总长已超过200万km，并且以每年4～5万km的速度递增。我国的管道工业在近20年内也得到了较大的发展，根据“十二五”规划，国内油气管道干网、支干网长度将由2010年的8万km提升至15万km。

目前世界上大部分管道已运行30～40年的时间。由于腐蚀、焊缝缺陷、震动及冲刷等原因引起的管道泄漏和法兰、螺纹扣及填料函等管道连接部位的泄漏变得日益严重。管道泄漏不仅会影响管输的正常进行，而且当输送有毒害、腐蚀性、易燃易爆的介质时，还会污染环境，引起火灾爆炸事故。因此，对管道泄漏的预防及泄漏的及时报警、定位具有极为重要的现实意义。

对管道泄漏检测方法的研究已有几十年的历史。为及时检测输油管道的泄漏，人们采取了多种方法，包括流量平衡法、基于模型的检测方法及瞬态压力波方法等。在这些方法中，大多数都需要进行管道压力和流量信号的采集。因此，对于采集的信号进行有效的去噪处理，正确提取有用的泄漏信息，提高泄漏检测系统的可靠性和定位精度是管道泄漏检测系统的重要设计指标。^[26]

小波变换的多分辨分析技术使得小波分析在时域和频域中都具有良好的分析能力，通过小波阈值去噪去除采集信号中的工况噪声，是提高管道泄漏检测灵敏度的有效方法；目前常用的泄漏点定位方法是瞬态压力波法，但是由于计算压力波传递到管道始末两端的时间差包含较大的误差，从而导致泄漏定位的误差较大。当输油管道发生泄漏时引起的压力和流量变化是典型的奇异点，通过小波变换的多尺度功能将信号的突变或瞬态特征进行提取，可以准确地确定奇异点的位置，也就有效提高了压力波传播时间差的测量精度，从而可以提高管道泄漏点的定位精度^[27]。

1.信号的奇异性

通常信号发生突变的时刻称为信号的奇异点，信号突变点（奇异点）的产生，通常是由于信号在某一时刻幅值或频率发生突变而引起了信号的不连续，或者是信号的一阶微分不连续所产生的。数学上常用李普西兹（Lipschitz）指数β来描述函数的局部奇异性。

李普西兹指数定义：如果函数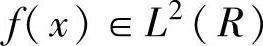对点x₀的某领域中任何x都有

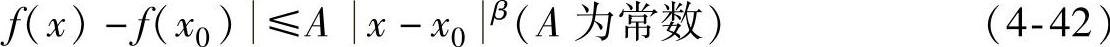
则称β为在x₀处的Lipschitz指数。如果对所有x，x₀∈（a，b），式（4-42）都成立，则称f（x）在（a，b）上一致Lipschitz β。

Lipschitz指数β给出了信号f（x）在x₀点光滑性的精确信息，如果β=0则函数f（x）在该点间断，有奇异性；如果β=1，则函数f（x）没有奇异性；如果0＜β＜1，函数f（x）的光滑性下降。β越大，则说明函数f（x）越接近规则；β越小，说明函数f（x）在x₀处变化越尖锐。阶跃函数在阶跃点β=0，脉冲函数β=-1，说明这两点都是奇异的^[28]。

2.小波奇异性理论

对于连续信号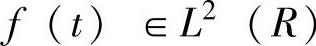（能量有限空间），f（t）的连续小波变换（CWT）定义为

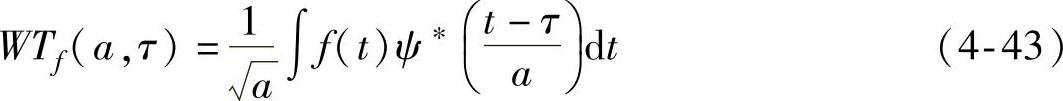
式中，ψ（t）为基本小波或母小波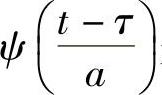，是依赖于a、τ的连续小波基数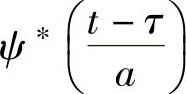，表示的共轭，a为小波变换尺度因子（a＞0），τ为小波变换的延伸因子，WT_f（a，τ）是对连续信号f（t）的连续小波变换。

在信号检测中，为了使用方便，通常采用卷积形式的小波变换，取尺度

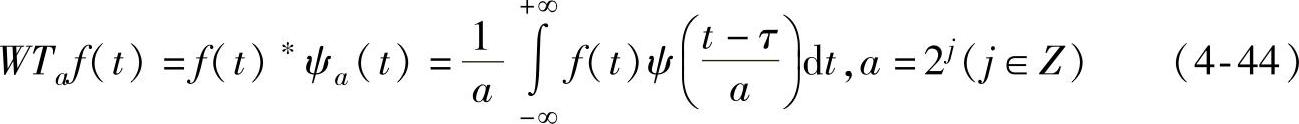
式（4-44）的小波变换被称为卷积形式的二进小波变换。它是测低能量的短暂瞬变信号的有效手段，非常适用于检测突发性泄漏引起的瞬态负压波。压力信号的突变点通常在信号的一阶或高阶导数中反映出来。在各种小波函数中，高斯函数的一阶导数对于信号的奇异点最为敏感。因此，选用高斯函数作为小波变换中的小波函数。高斯低通函数为

3.小波变换模极大值在多尺度上的表现与Lipschitz指数的关系

在不同的尺度a_i（i=1，2，3，…n）下，对信号f（t）进行的连续小波变换。

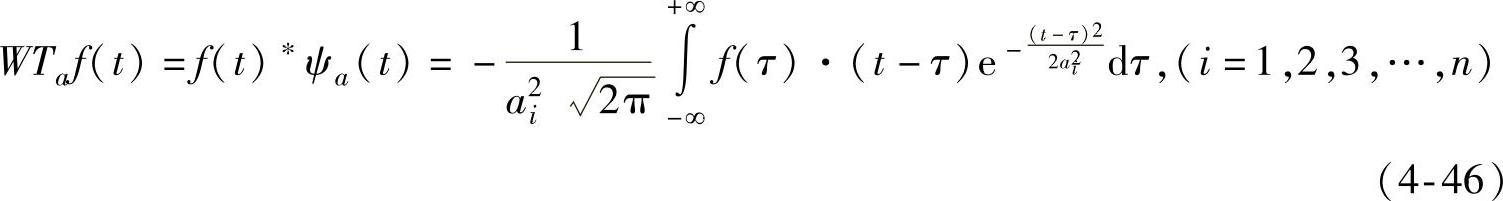
定义：在某一尺度a₀下，如果存在一点（a₀，τ₀）使得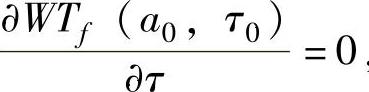，则称点（a₀，τ₀）是局部极值点，对于τ₀的某一邻域的任一点τ，有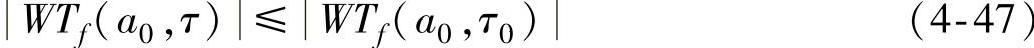则称（a₀，τ₀）为小波变换模极大值点。(www.xing528.com)

Mallat已经证明：t在区间[a，b]中时，如果f（t）的小波变换满足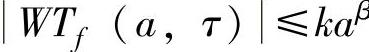：也就是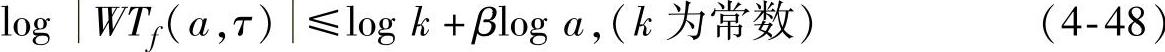

当尺度a=2^j时（j为小波变换的尺度特征），式（4.6.2–7）变成WT_f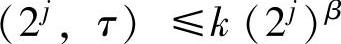，取2为底数的对数，则有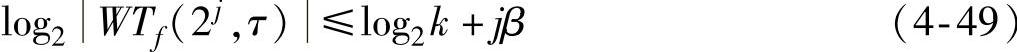

由式（4-48）可以看出，小波变换模极大值将随着变换的尺度a以及信号的Lipschitz指数β的变化而变化。当β＞0时，小波变换模极大值将随尺度的增大而增大；当β＜0时，则随着尺度凸的增大而减小；β=0时，则小波变换的模极大值不随尺度改变。

噪声和有用的信号边沿都具有奇异性，但是噪声对应的Lipschitz指数远远小于0，而有用信号边沿对应的Lipschitz指数大于或等于0，根据（4-49）式的分析可知，噪声和信号边沿在多尺度连续小波变换下的极值具有截然不同的表现，噪声对应的小波变换的极值将随着尺度的增大而迅速衰减，而信号边沿所对应的小波变换的极值将随着尺度的增大而增大或保持不变。这样，就可以利用连续小波变换从噪声背景中准确地分离出信号边沿。

对奇异点进行检测定位，一般采用二进小波变换由粗到细的算法，跟踪各尺度下小波变换模极大值，先从最粗尺度的一级开始，找到这一尺度上属于信号的小波变换模极大值，然后逐步减小尺度值，直到逐级搜索到最细尺度为止。由于尺度不同，小波函数的特征值会发生一些变化，引起高频细节中模极大值发生微小偏移，可以采用均值法，取模极大值的均值。平均处理后的小波变换结果既保留了比较准确的峰值位置和比较窄的尖峰形状，又很好地去除了伪极值。

4.小波模极大值方法在管道泄漏检测与定位中的具体应用

（1）管道泄漏检测系统组成

系统主要由下位机、通信模块、上位机组成。下位机为数据采集系统，主要完成现场数据的采集，定时向数据采集模块发送采集命令，数据采集模块返回管道参数（压力），同时从GPS校时器获得CPST标准时间，由管道参数和时间标签构成一段数据，由多段数据构成了一个传输文本，等待上位机传输命令。通信模块完成上位机与下位机的通信功能，通过公用电话网实现对多数据传输，上位机通过MODEM轮流接通下位机MODEM后，向下位机定时发送传输命令，并接收下位机数据。上位机为放置在中央控制室的一台工控机，工控机对采集上来的压力信号以曲线的形式进行实时显示，并根据输油管道两端的压力采集信号，对输油管道中出现的泄漏及时进行报警和漏点定位。

（2）泄漏检测与定位

当管道发生泄漏时，泄漏点附近会产生压力突降，这一压力变化以负压波的形式向管道两端传播。通过分析管道两端的压力信号可以判断泄漏的发生，并根据两端压力突降点出现的时间差进行泄漏的定位。可见，在输油管道泄漏检测系统中，准确捕捉到管道首末两端压力变化的突变点，即负压波到达管道首末两端的时刻，是负压波法检测管道泄漏的关键。

5.小波模极大值法在定位管道泄漏位置的关键技术

1）信号的局部奇异性由小波变换的模极大值点来描述，但并非所有的模极大值点都对波形识别具有重要意义。为了提取信号主要特征，需要对模极大值点进行提炼，保留真正反映原始信号主要特征的模极大值点，去除噪声产生和次要的模极大值点。通过检测小波变换的模极大值点的幅值沿尺度的演变规律，可以将噪声所产生的模极大值点与信号所产生的模极大值点区分开来。因此，为了对信号产生的奇异点进行准确定位，需要对噪声或次要的模极大值曲线进行过滤。

2）为了精确计算负压波到达首末两端的时间差，提高泄漏点的定位精度，管道首末两端系统时间必须保持一致。采用GPS定时，可使两端计算机的时间同步到毫秒，定位精度将进一步提高^[28]。

6.小波变换去噪实例

在输油管道上不同位置施加冲击激励，测量到不同的响应波形。图4-17a、b、c分别为距离传感器300m、800m和1200m处所得应力波波形。显然，4-17a所示的波形的信噪比最小，进行波达时刻判断最难，因此，本章选择该波形进行验证。选用coif5小波，分解级数为5，coif5是一种紧支撑的正交小波基，比较适合文中冲击应力波的分解。得到5级分解下的小波系数分别为d1～d5。分析发现，系数中的d1～d3主要为高频噪声引起，随着尺度的增大，其模极大值点的稠密度（单位长度下模极大值点的个数）逐渐变少，而冲击应力波波形的小波系数的模极大值随尺度的增大逐渐明显起来。在d4、d5下表现突出。为了消除随机噪声的影响，应该去掉d1、d2、d3的小波系数，保留部分d4和d5的小波系数。为此，分别选取0.020、0.021、0.021、0.021、0.021为d1～d5的阈

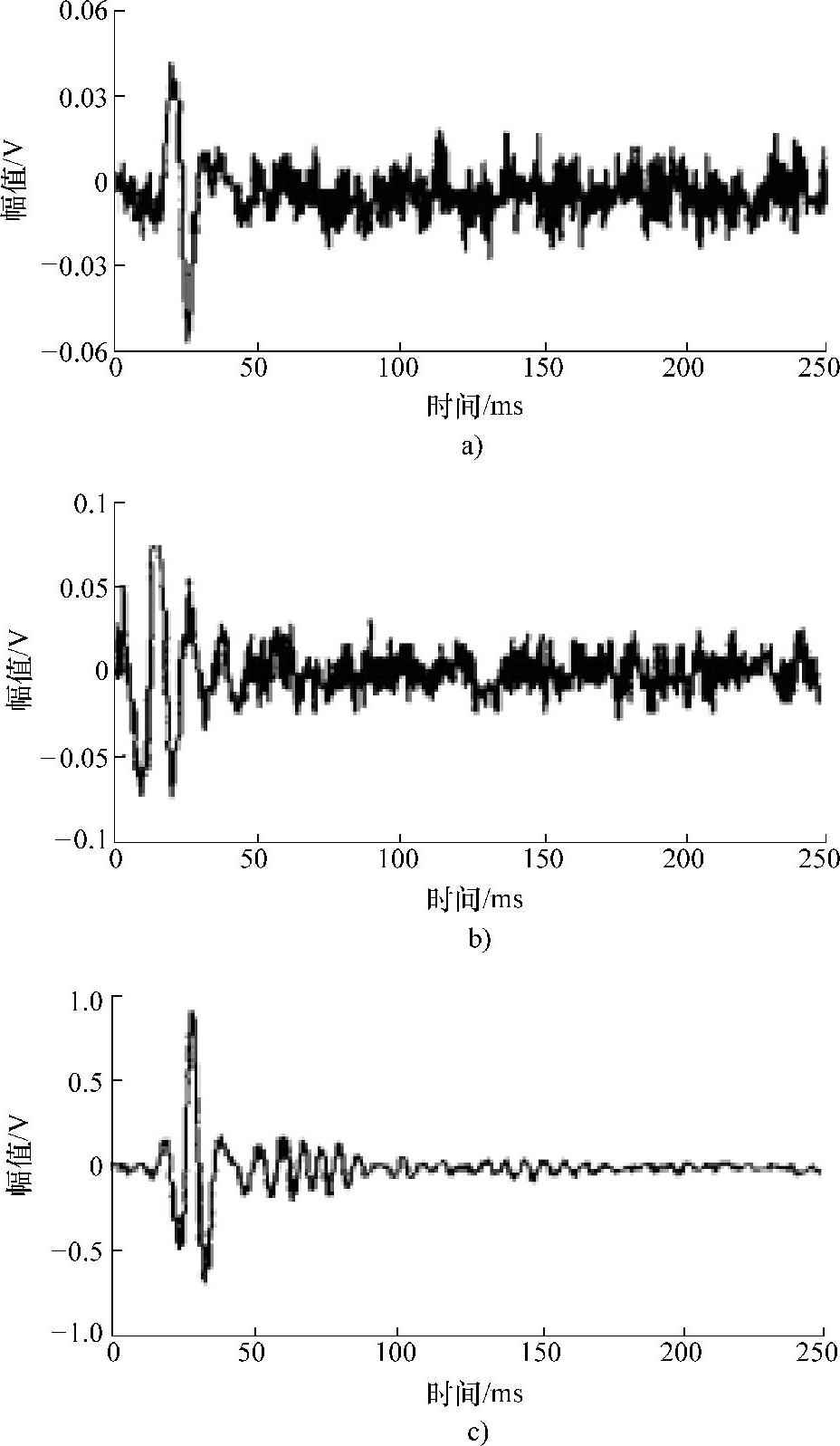
图4-17 不同距离处实测应力波原始波形

值。保留模值超过阈值的小波系数，其余系数置零。利用高于阈值的小波系数进行信号的重建，便得到去噪的结果，如图4-18所示。其中图4-18a所示为去除噪声后的信号波形，图4-18b所示为被去除的噪声成分^[29]。

图4-18 阈值去噪结果

小波变换是近年来发展起来的一种数学理论和方法。由于小波具有很高的时间和频率分辨率，可以用来进行奇异性信号的分析，将这种方法应用于管道泄漏检测技术中，可以有效地监控管道的运行状态，及时、准确地检测出管道的泄漏故障，排除工况的干扰。该检测方法不仅可以用于石油泄漏检测，也可以用于自来水管道的泄漏检测，具有很好的推广价值^[28]。