桥梁结构健康监测系统振动信号处理方法

结构的健康监测是指利用现场无损测量信息分析系统的特性参数，包括结构的响应，以识别结构的变化，从而揭示结构可能的损伤或质量退化。测量结构的应变、位移、转角、速度等参数，是结构评估的基本手段。它应用于航空航天、船舶工程、机械制造等许多行业，在现代土木工程领域，主要应用在大中型重要桥梁及在旧桥承载能力的评估方面。随着近20年来桥梁抗风、抗震领域的成果以及新材料、新技术的不断开发，极大地推动了大跨度桥梁的发展。人们也对其安全性、耐久性与正常使用功能日渐关注，因而桥梁结构的健康监测亦显得尤为重要。它可以在特殊气候、交通条件下或桥梁运营状况严重异常时发出预警信号，为桥梁维护、维修与管理决策提供依据和指导^[23]。

1.健康监测系统

大型桥梁健康监测系统一般应包括以下几部分内容：

（1）传感系统

传感系统由传感器、二次仪表及高可靠性的工控机等部分组成。

（2）信号采集与处理系统

信号采集与处理系统用于实现多种信息源、不同物理信号的采集与预处理，并根据系统功能要求对数据进行分解、变换以获取所需要的参数，以一定的形式存储起来。

（3）通信系统

通信系统将处理过的数据传输到监控中心。

（4）监控中心

监控中心可以利用可实现诊断功能的各种软硬件对接收到的数据进行诊断，包括结构是否受到损伤以及损伤位置、损伤程度等。

传感器监测到的实时信号，经过采集与处理曲通信系统传送到监控中心进行分析和判断，从而对结构的健康状况作出评估。若结构出现异常行为，则由监控中心发出预警信号，并对检测出来的损伤进行定性、定位和定量分析同时提供维修建议。

大型桥梁健康监测系统不单是传统的以人工方法为主的检测手段的简单改进，而是运用现代化传感设备与光电通信技术及计算机技术，实时监测桥梁在各种环境条件下的结构响应和行为。一般大型桥梁健康监测系统对以下几方面进行监控：结构的固定模态及其相对应的结构阻尼；桥梁在正常车辆荷载及风载作用下的结构响应和力学状态；桥梁在突发事件（如强烈地震、意外大风或其他严重事故等）之后的损伤情况；桥梁结构构件的真实疲劳状况；桥梁重要非结构构件（如支座）和附属设施（如斜拉桥振动控制装置）的工作状态；大桥所处的环境条件，如风速、温度、地面运动等^[24]。

2.振动信号的分析与处理

桥梁结构的健康状况是由测试的信号来监测和评估的，即从传感器采集的信号中提取各种特征，对结构进行参数检测、状态监控和损伤诊断等。但是，实测信号都不可避免地被各种噪声所污染，信噪比严重下降，故在后续诊断技术之前需要对实测信号进行必要的预处理。^[24]

振动信号预处理是指对数据采集系统得到的实测信号在分析前进行预处理，以提高数据的真实性和稳定性，从而选择合理的后续诊断技术。振动信号预处理，是结构健康诊断的首要步骤，它直接决定着后续诊断技术有使用效果及精度。一般来讲振动信号预处理方法有以下几种思路：

1）数据的奇异值点剔除：即对数据中异常的极值进行消去、修复，以及对双极性振动信号中的局部单极性进行修正。

2）多段数据线性平均：指在数据量很大的情况下，对多段信号进行累加、平均处理，去除随机信号的干扰。

3）数字滤波：在振动信号分析中，数字滤波是指通过数学运算从所采集的离散信号中选取感兴趣的一部分信号进行相应的滤波处理。它的主要作用是滤除测试信号中的噪声或虚假成分、提高信噪比、平滑分析数据、抑制干扰信号、分离频率分量。

这些预处理方法对于旋转机械的诊断，有着十分显著的作用。而其中数字滤波器对处理随机信号也显得很困难。对于以地震为代表的随机信号，这些信号预处理方法却存在着一定的不足，原因是这些随机信号中存在着许多具有重要的瞬态突变信号。对这些信号进行分析时，往往要去除一些高频信号的干扰，上述预处理方法在去除高频信号的同时，或者减弱了突变信号，或者改变了突变信号的幅值分布。这样，这些方法必然影响了后续分析方法的精度。

振动信号预处理主要包括两方面：一是减少或消除采集数据中的干扰成分，如多项式趋势项；二是对原始信号做适当的数据平滑处理。所谓多项式趋势项就是在随机振动中存在的线性项或长周期的非线性成分。多项式趋势项主要是针对随机信号的，但在确定性信号中也存在趋势项。趋势项的存在，会使时域相关分析产生较大的误差，甚至使频域频谱产生严重的失真。另外，由于随机干扰信号频带宽，高频成分有时所占比例大，使得由采集数据描绘的振动曲线呈现大范围的毛刺，故需对采集数据做平滑处理，提高信噪比和曲线光滑度。

下面讨论了振动信号预处理的两种方法，消除多项式趋势项和数据平滑处理。这两种振动信号预处理方法为振动信号的预处理提供了新的途径，它们可以在最大限度的保留实测信号的前提下，对振动信号进行光滑处理，从而去除高频噪声干扰。

3.消除趋势项

对加速度信号进行积分变换求测点的位移和速度是振动信号处理中常用的方法。由于信号中的低频成分对位移振动幅值的大小起着决定性的作用，而在测试信号中往往因测试仪器温度变化造成的零点漂移含有长周期趋势项，在对数据进行积分变换时，趋势项对变换结果的影响比较突出，在对数据进行二次积分，由于长周期趋势项的存在，得到的变换结果可能完全失真。同时从传感器输出的原始信号有时只有毫伏数量级，不满足模数转换器的分辨率，故需对传感器的输出信号通过放大器进行放大处理。由于放大器随温度变化产生的零点漂移以及传感器周围的环境干扰（如温度、湿度、电磁场、噪声、射线等），实测信号会偏离基线，甚至偏离基线的幅度是时间的函数。偏离基线随时间变化的整个过程就称作信号的趋势项。趋势项直接影响实测信号的真实性，可见消除趋势项是振动信号预处理的一个重要内容。本文采用多项式最小二乘法消除趋势项。

最小二乘法是一种用解析表达式来对实测数据进行数值计算拟合的算法。通过它能获得在最小平方差意义上的测试数据与数学模型的最佳拟合。最小二乘法既可消除数字信号中的线性趋势项，又可消除非线性高阶多项式趋势项。

数据采集系统得到的振动信号为{x_k}（e=1，2，…，N），是按等时间间隔采样，令采样时间间隔Δt=T，为算法推导方便，这里取T=1。选择M阶次多项式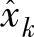来拟合采样信号x_k，则有

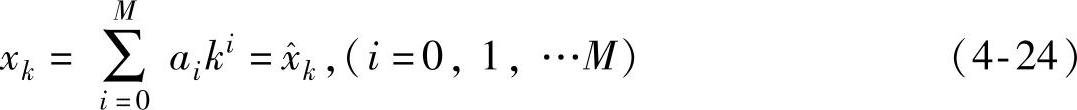
根据最小二乘法原理，选择合适的系数a_i（i=0，1，…，M），使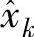和x_k间的误差二次方和最小，其误差二次方和为

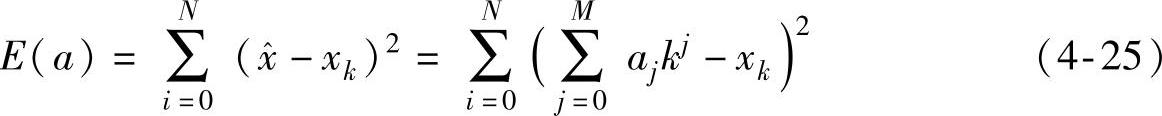
根据最小二乘法原理中的极值条件，E（a）对a_j的偏导数就等于零，即

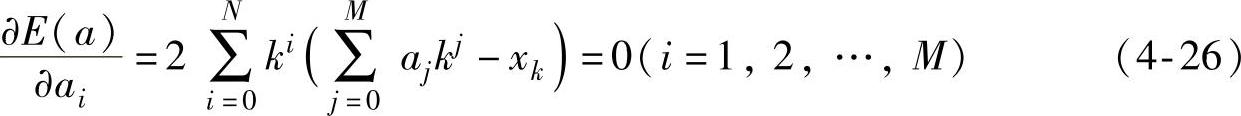
依次取E（a）对a_i求偏导数，可以得到一个M+1元线性方程组：

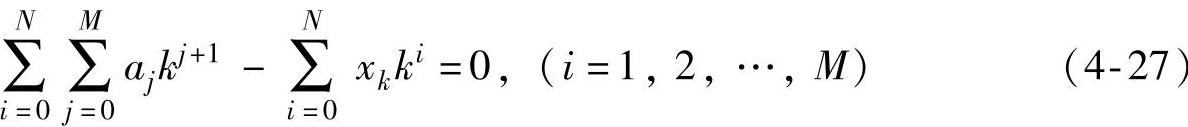
解方程组（4-27），求出M+1个待定系数a_j（j=0，1，2，…，M）。M=0时的趋势项为常数，有

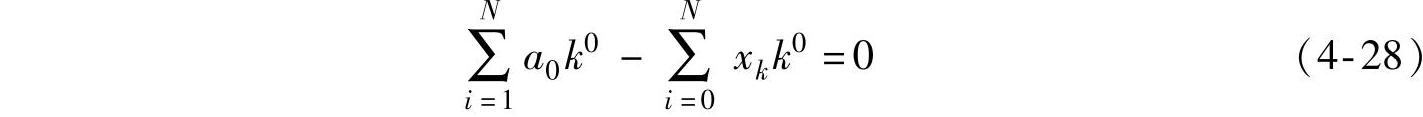
解方程组(4-28)，得

从式（4-29）可知，M=0时的趋势项为采样信号的算术平均值。消除常数趋势项的算子为

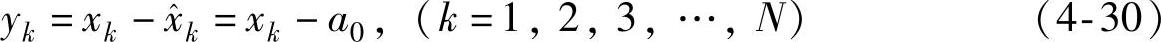
M=1时为线性趋势项，有(www.xing528.com)

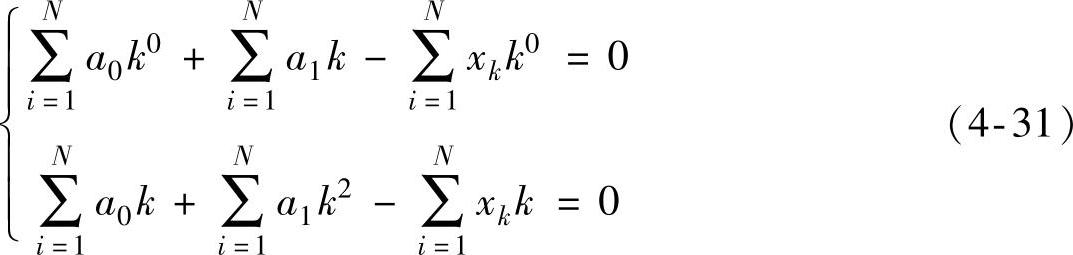
解方程组（4-31），得

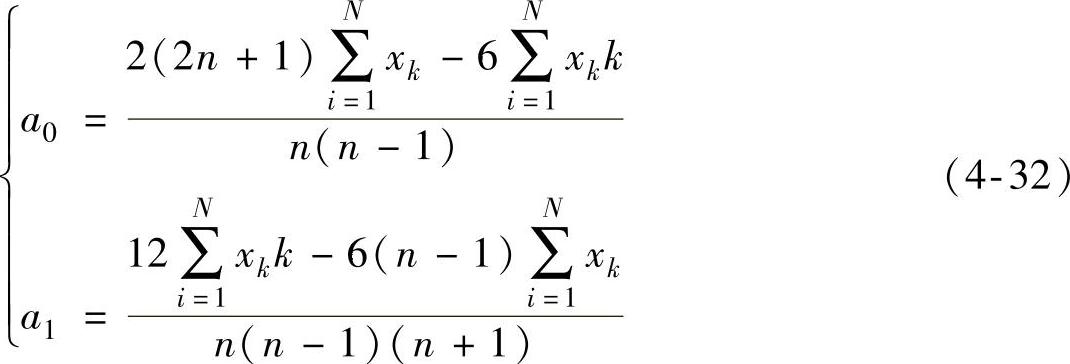
消除线性趋势项的算子为

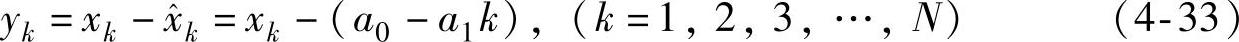
M≥2时为曲线趋势项。在实际振动信号数据处理中，M一般不要大于3，通常取M=1～3对采样数据做多项式趋势消除处理。

4.数据平滑处理

数据采集系统得到的振动信号中常混叠有噪声信号。噪声信号除了周期性的干扰信号处，还有不规则的随机干扰信号。由于随机干扰信号的频带较宽，甚至有时高频成分所占比例很大，使得由采集到的离散数据绘制成的振动信号波形上呈现许多毛刺，很不光滑。另外，在振动测试过程中，有时测试仪器由于受到某些意外干扰，造成个别测点的采样信号偏离基线较大，形状极不规则。数据平滑处理主要是为了削弱或消除干扰信号，提高信噪比和曲线光滑度。本文采用五点三次平滑法处理数据。

五点三次平滑是在等间距数值的基础上对数据进行处理的一种方法，设y为x的函数，用泰勒公式将y展开为幂级数形式，按精度要求一般取前四项，即

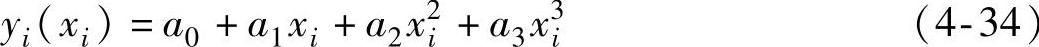
其方差和为

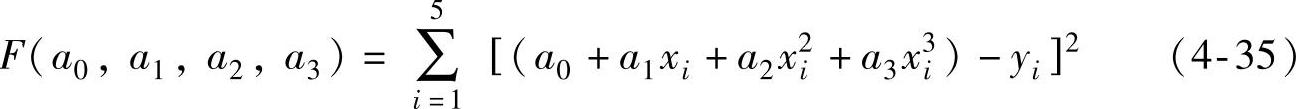
要求式（12）取极小值，根据最小二乘法原理，即

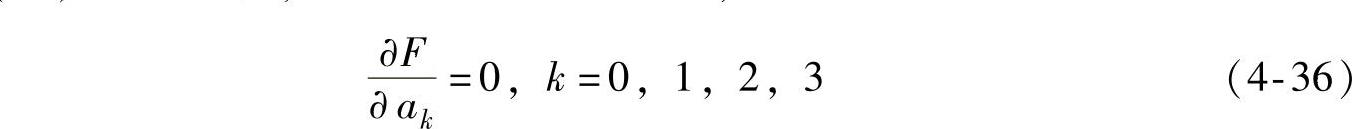
将式（4-36）展开可得到

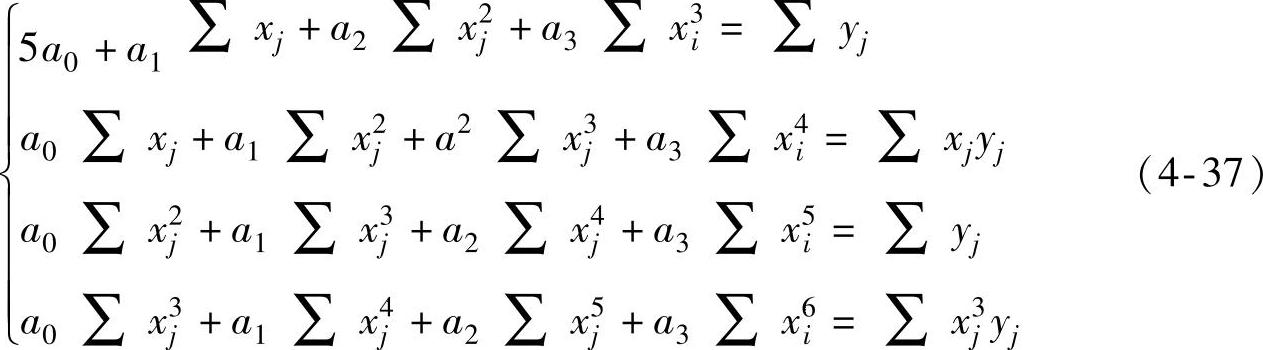
式（4-37）中，j=i-2，i-1，i，i+1，i+2因为是等距离数值，不妨取x_i=0，则相应的五点的x值分别为-2Δx，-Δx，0，Δx，2Δx，因此，可以得到以下关系式：

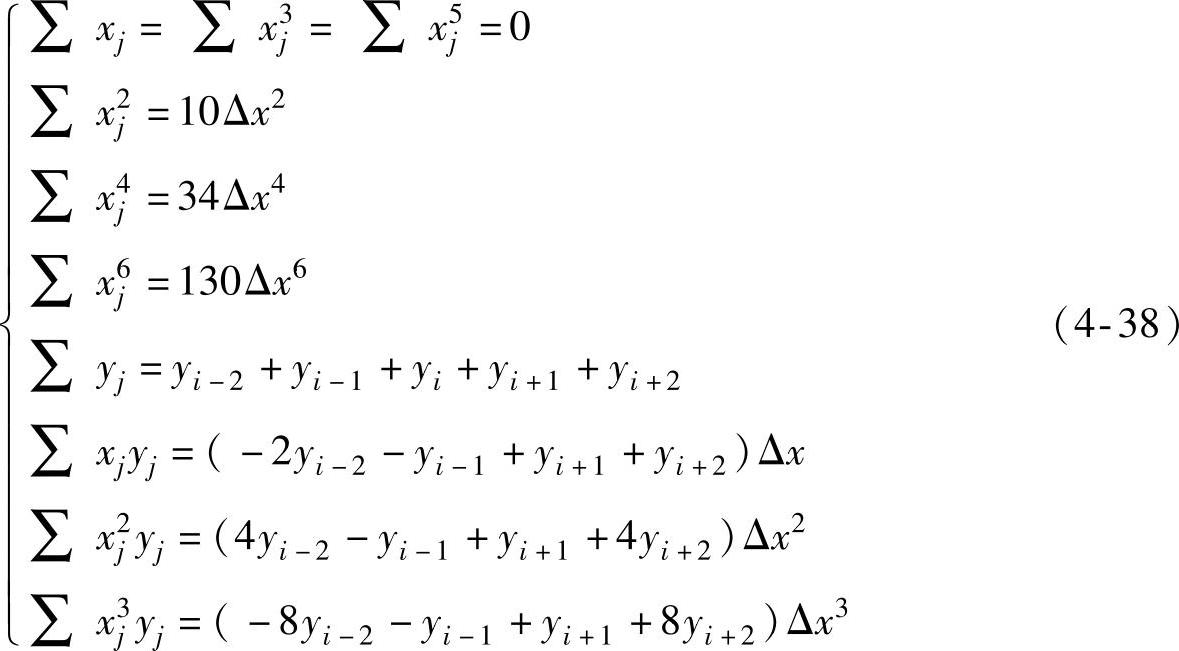
联立方程组（4-37）与（4-38），解出a₀，a₁，a₂，a₃值分别为

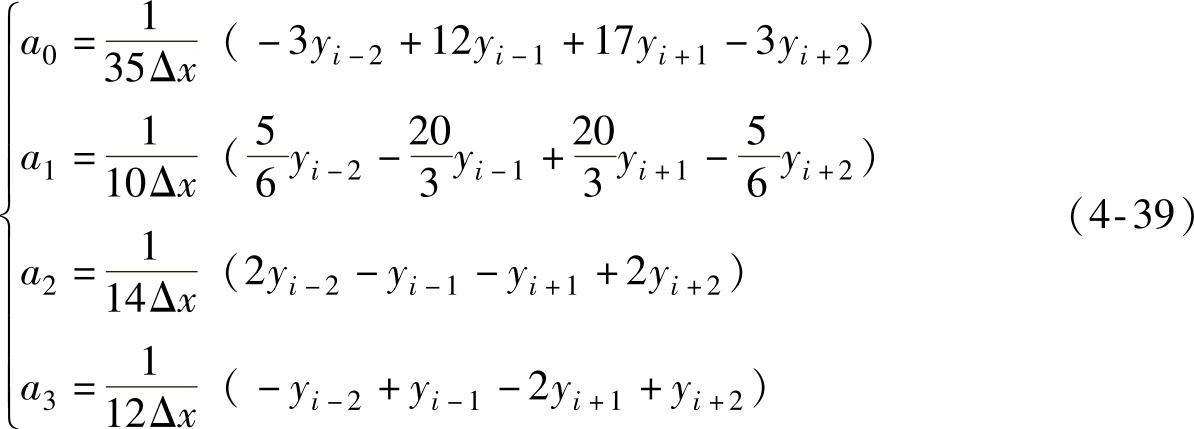
将所取的x的值-2Δx，-Δx，0，Δx，2Δx分别代入式（4-34）得

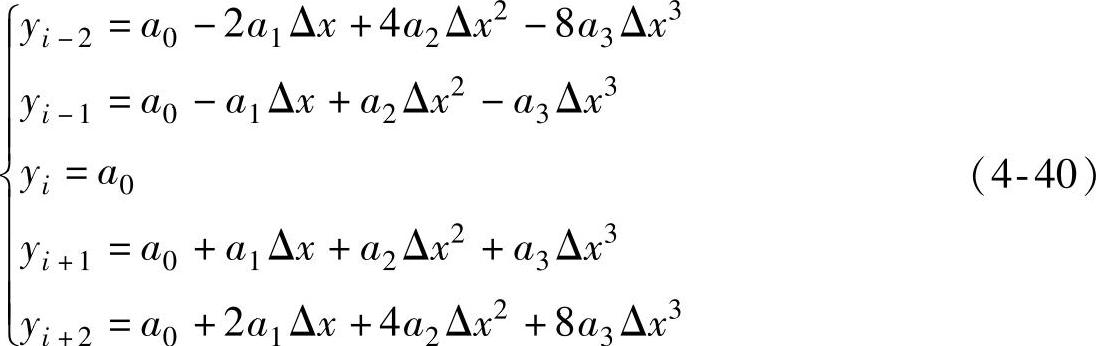
再把式（4-39）代入式（4-40），可得五点三次平滑法的计算公式为

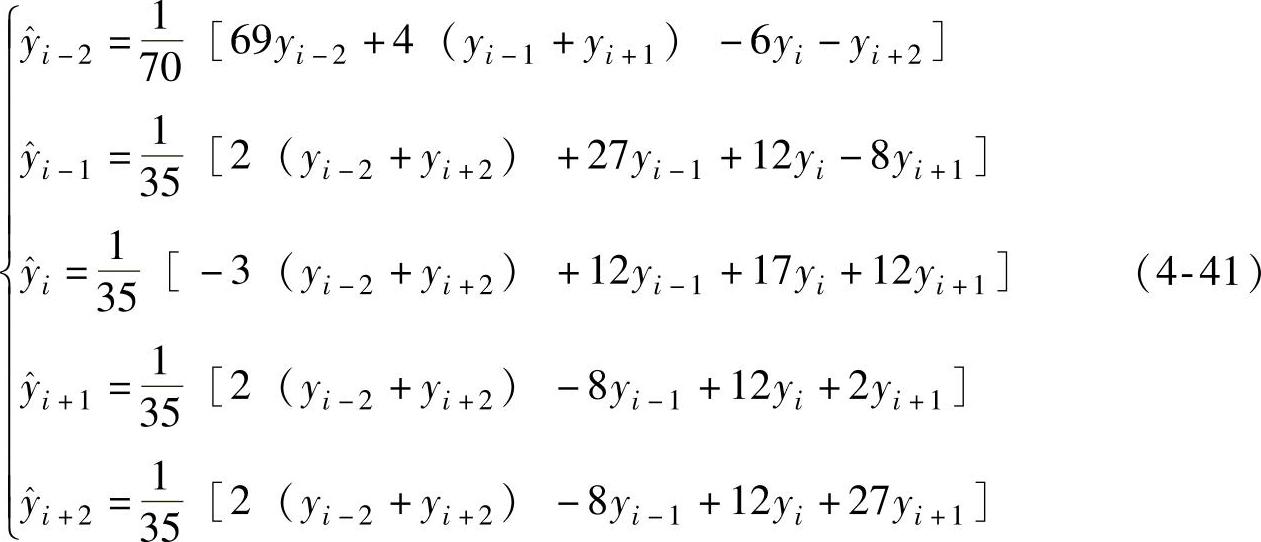
由公式（4-41）也可以看出，处理后的数据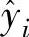只与处理前的y_i及其前后的共五个数值有关，与x_i及间隔Δx都没有关系，故只要是等间隔的数据都可以用这种方法来进行处理。

国内外许多研究表明，若能从采样信号中很好地提取地震信号，就能正确掌握地震动的主要参数，时程分析结果就可以真实地体现未来地震作用下的结构反应。本文以MATLAB为开发平台，分别以两个著名的地震波El_centro、Taft为例，分别如图4-11和图4-12所示，对上述两种算法进行验证。计算结果见图4-13～图4-16。

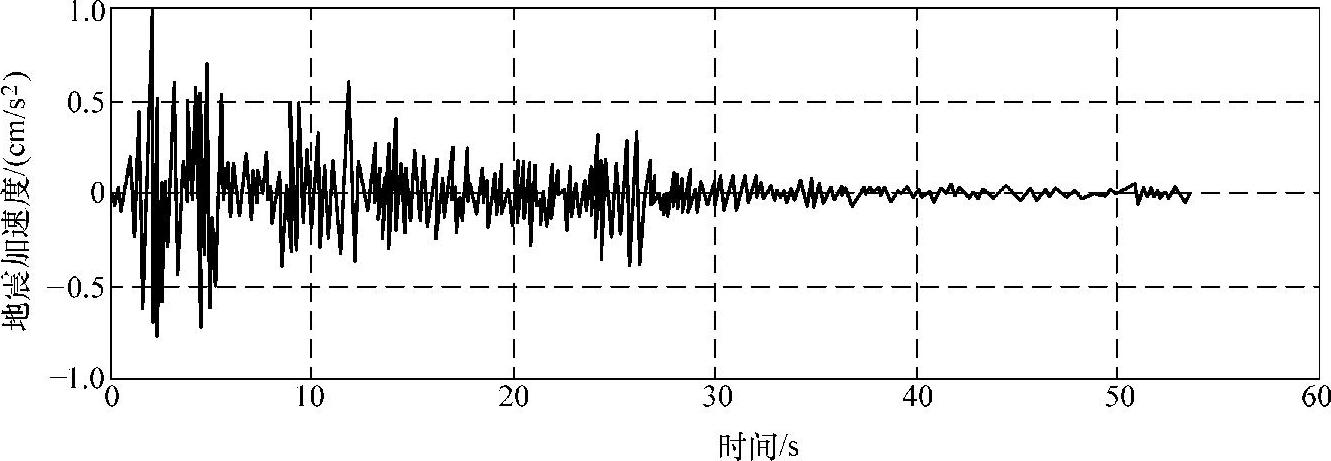
图4-11 地震波El_centro波形

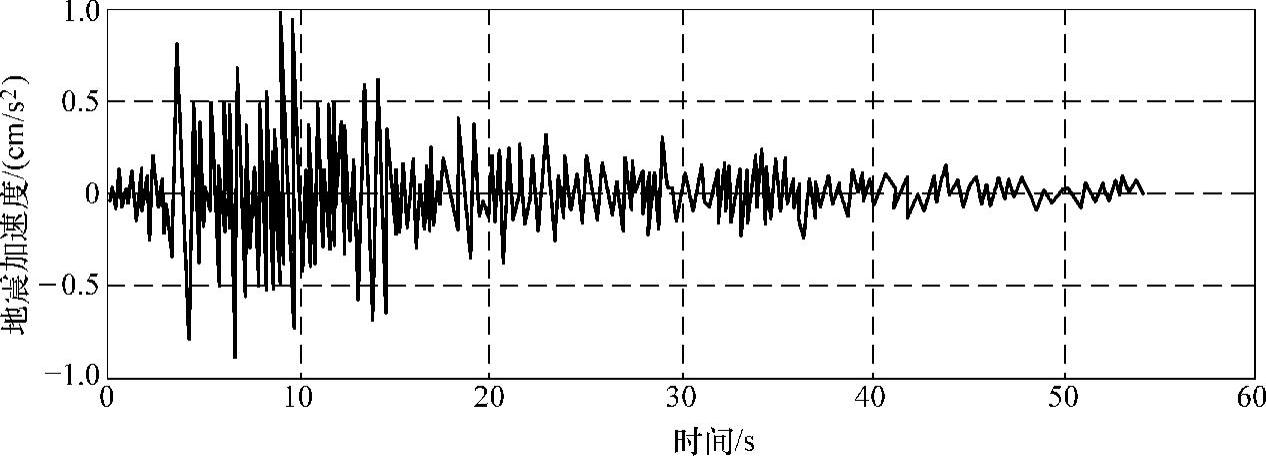
图4-12 地震波Taft波形

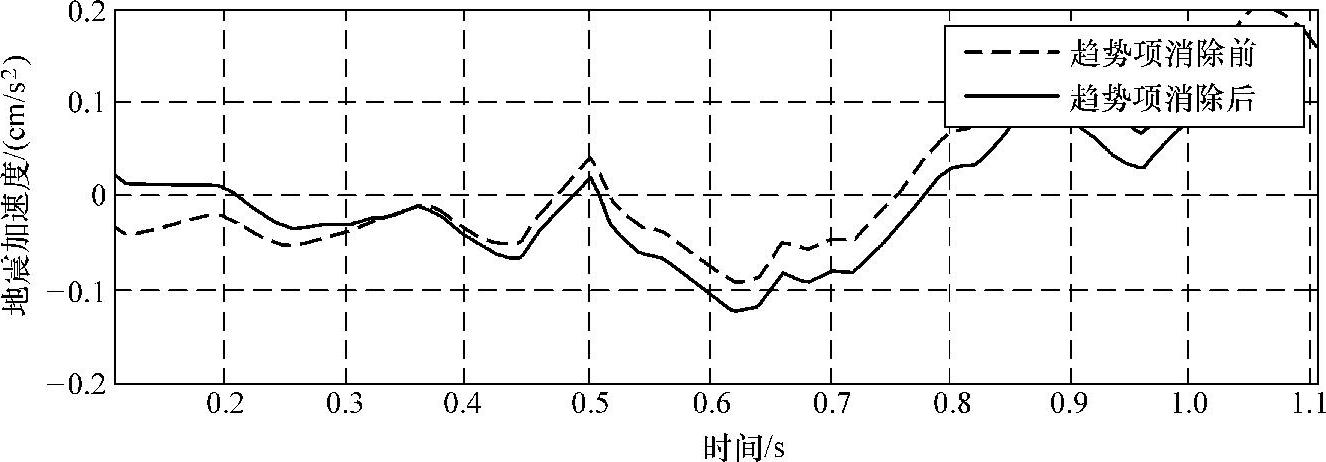
图4-13 El_centro波趋势项消除前后的波形

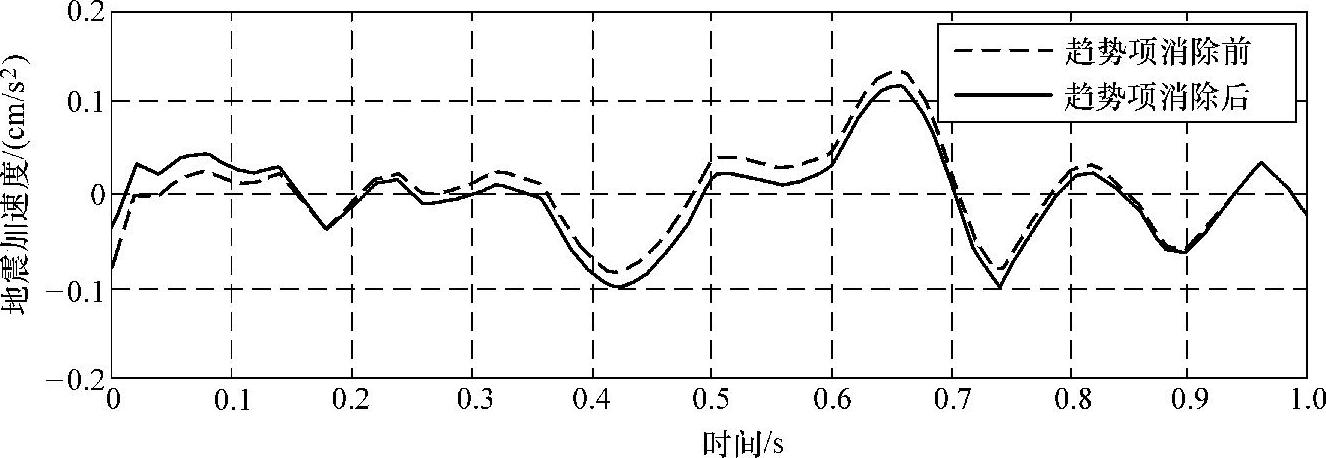
图4-14 Taft波趋势项消除前后的波形

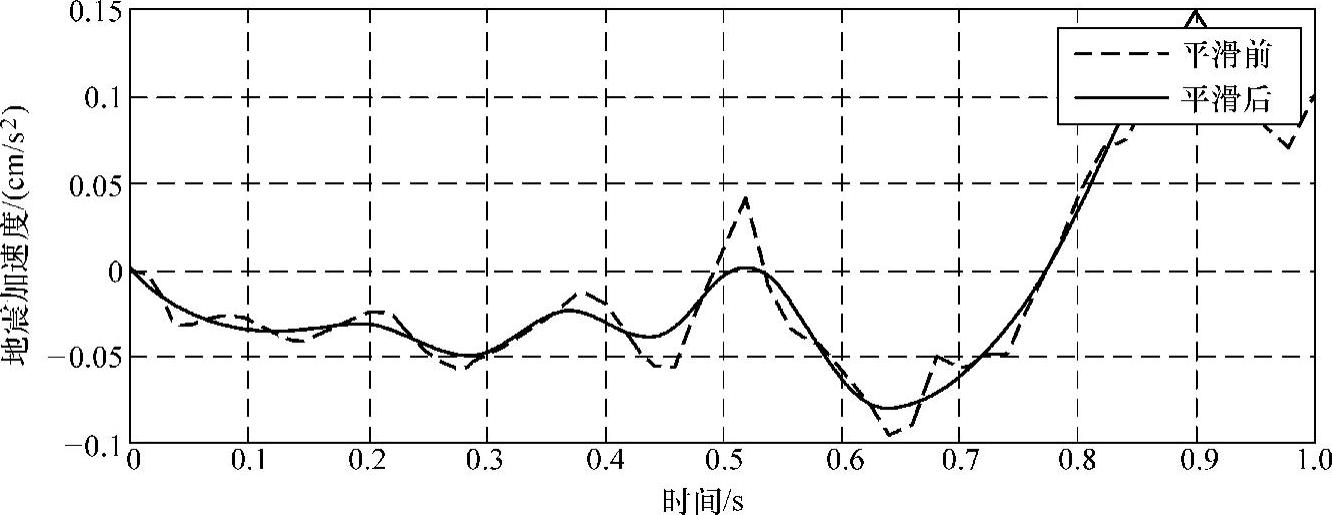
图4-15 El_centro波五点三次法前后的波形

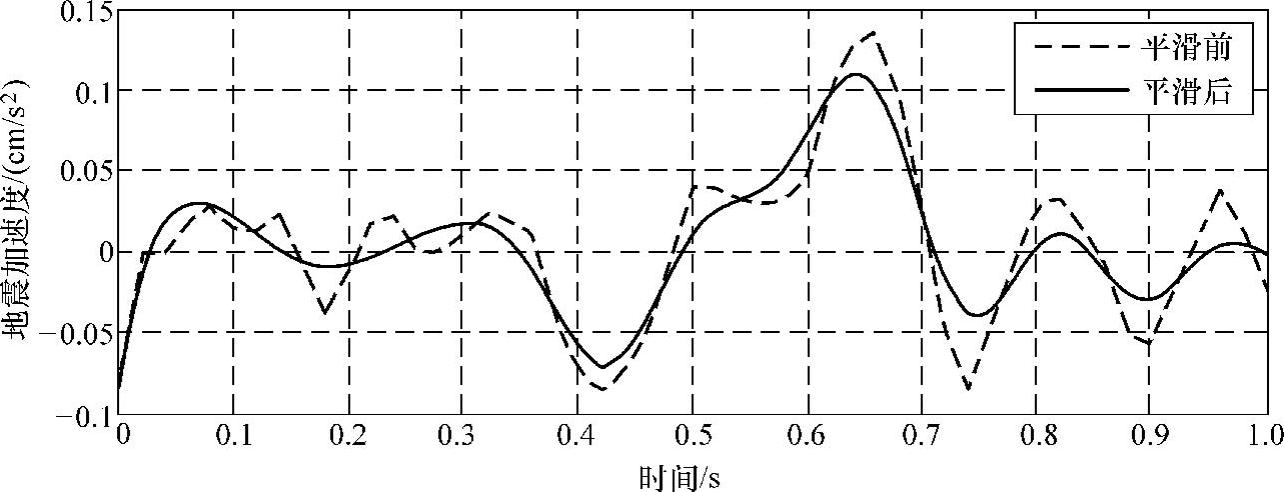
图4-16 Taft波五点三次法前后的波形

由上述几幅图可知，两种方法都有效地提高了地震波信号的质量。由图还可以看出，消除多项式趋势项处理后的波形数据比较贴近实测数据，而五点三次平滑法处理后数据的波形更光滑，但个别点与实测数据相差较大。五点三次平滑法可以用作时域和频域信号平滑处理，该处理方法对时域数据的作用主要是能减少混入振动信号的高频随机噪声。而对于频域数据的作用则是能使谱曲线变得光滑，以便在模态参数识别中得到较好的拟合效果。但需要注意的一点是频域数据经过五点三次平滑法会使得谱曲线中的峰值降低，体形变宽，可能会造成识别参数的误差增大，故平滑的次数不宜过大。在工程实际应用中，要根据具体情况选择最适合的算法^[25]。