多传感器信息融合方法-监测系统中智能信息处理技术

多传感器信息融合的最重要的部分是信息融合的方法，应用上的多样性和复杂性决定了信息融合的丰富性，它涉及的基础理论较多。因此，多传感器融合系统的核心问题是选择合适的融合方法。多传感器信息融合方法可以分为估计方法、分类方法、推理方法和人工智能方法四类，如图4-10所示。

在估计方法中，加权平均法是最简单、最直观的一种方法，该方法直接对数据源进行操作，它将一组传感器提供的冗余信息进行加权平均，将得到的结果作为融合值。卡尔曼滤波是另外一种应用较多的估计方法，主要用于融合低层次实时动态多传感器冗余数据。卡尔曼滤波方法用测量模型的统计特性递推从而决定统计意义下的最优融合和数据估计。如果检测系统具有线性动力学模型，并且系统以及传感器的误差符合高斯白噪声模型，则卡尔曼滤波将提供唯一统计意义下的最优估计。卡尔曼滤波的递推特性使系统处理不需要大量的数据存储和计算。但是，采用单一的卡尔曼滤波器对多传感器数据进行统计时，存在很多严重的问题：在组合信息大量冗余的情况下，这种方法的计算量将以滤波器维数的三次方剧增，实时性不能满足；传感器子系统的增加将增加故障的可能性，在某一系统出现故障而没有来得及被检测出时，故障会传递到整个系统，从而使得系统的可靠性降低。

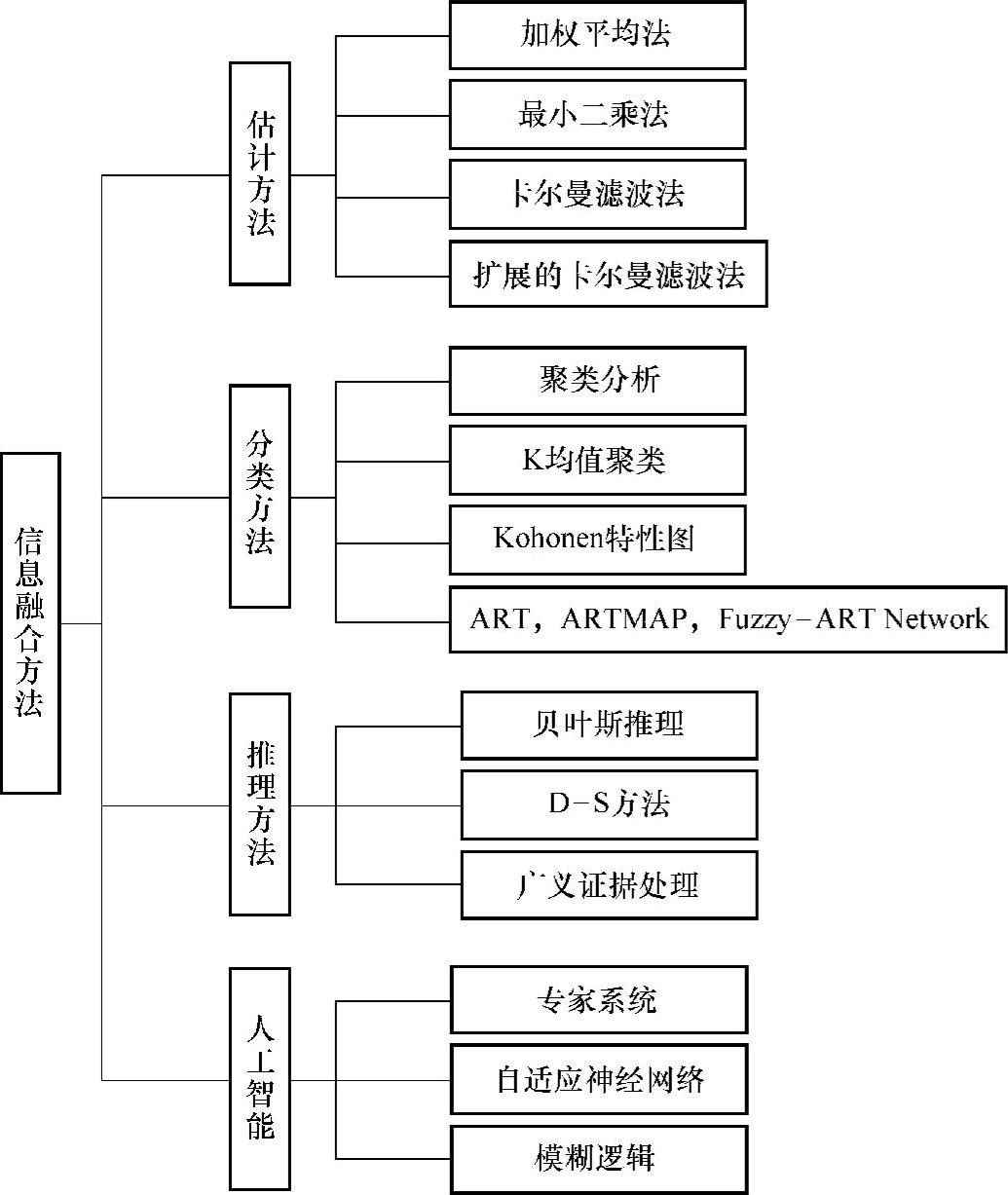
图4-10 多传感器融合算法分类

分类方法中应用较多的是参数模板法和聚类分析法。此外，自适应共振理论（ART）、自适应共振理论映射（ARTMAP）和模糊自适应共振理论网络（fuzzy-ART network）以自适应的方法进行传感器融合。这些方法能够自动调整权值，稳定性较好，能在环境变化和输入漂移的情况下保持稳定。除此之外，学习向量量化法（Learning Vector Quantization，LVQ）、K均值聚类（K-means Clustering）、Kohonen特性图（Kohonen Feature Map）等这些无监督或自组织学习算法也常用作多传感器数据的分类。K均值聚类算法是最常用的无监督学习算法之一，而自适应K均值聚类方法的更新规则构成了Kohonen特性图的基础。

推理方法包括贝叶斯推理、D-S证据推理方法以及广义证据处理方法。贝叶斯推理法是融合静态环境中多传感器信息的常用方法。它将多传感器信息依据概率原则进行组合，然后测量其不确定性并以条件概率表示，当多个传感器的观测坐标一致时，该方法可以直接对传感器的数据进行融合。但大多数情况下，多传感器测量数据要以间接方式采用贝叶斯推理进行数据融合。在多贝叶斯推理法中，每一个传感器被当作一个贝叶斯估计。该方法将各个单独传感器的关联概率分布合成为一个联合的后验概率分布函数，通过使得联合分布函数的似然函数为最小，来提供多传感器信息的最终融合值，融合信息与环境的一个先验模型则提供了整个环境的一个特征描述。D-S证据推理是贝叶斯推理的扩充，它包含三个基本要点，即基本概率赋值函数、信任函数和似然函数。D-S方法的推理结构自上而下可分为三级：第1级为目标合成，该级把来自独立传感器的观测结果合成为一个总的输出结果（ID）；第2级为推断，这一级获得传感器的观测结果并进行推断，并将传感器观测结果扩展成目标报告。这种推理的基础是：一定的传感器报告以某种可信度在逻辑上会产生可信的某些目标报告；第3级为更新，它的作用是更新传感器的观测数据。各种传感器一般都存在随机误差。所以，在时间上充分独立地来自同一传感器的一组连续报告比任何单一报告更加可靠。因此，在推理和多传感器合成之前，要先组合（更新）传感器的观测数据。

人工智能方法主要包括专家系统、自适应神经网络和模糊逻辑三种。专家系统是一种基于人工智能的计算机信息系统。而自适应神经网络则是一个具有高度非线性的超大规模连续时间自适应信息处理系统。在多传感器融合系统中，各信息源提供的环境信息都具有一定程度的不确定性，对这些不确定信息的融合过程实质上是一个不确定性推理过程。神经网络可根据当前系统所接受的样本的相似性，确定分类标准。同时可以采用特定的学习算法来获取知识，得到不确定性推理机制，因此可得到较好的效果。模糊逻辑是一种多值逻辑，它将传感器信息融合过程中的不确定性直接表示在推理过程中。由于模糊集表达了一个不确定概念，应用模糊理论并结合其他手段，如神经网络，往往可以取得更好的融合结果^[20]。(https://www.xing528.com)

表4-5为常用的数据融合方法在信息类型、信息表示、不确定性、融合技术及适用范围等方面的比较。

表4-5 常用的数据融合方法比较

（续）