【摘要】：为了更好地描述非平稳信号幅频特性随时间的变化情况，可以直接用信号的时频二维分布对信号进行描述，魏格纳分布就是一种常用的二次型时频分布。WVD是一种重要的二次时频分布，具有高分辨率、能量集中性和满足时频边缘特性等许多优良特性。这些方法对交叉项的抑制起到了很大作用，但是已经证明，不含交叉干扰项且具有WVD聚集性的时频分布是不存在的。二次型时频分布还包括魏格纳时频谱和小波尺度谱等。
为了更好地描述非平稳信号幅频特性随时间的变化情况，可以直接用信号的时频二维分布对信号进行描述，魏格纳（Wigner）分布就是一种常用的二次型时频分布。Wigner分布最初是由E.P.Wigner于1932年提出，并应用于量子力学领域。1948年J.Ville将Wigner分布引入到信号处理领域，提出了有名的Wigner-Ville分布（Wigner-VilleDistribution，WVD）。对任一可测的、二次方可积的信号x（t）∈L2（R），其WVD定义为
式中，WVD中的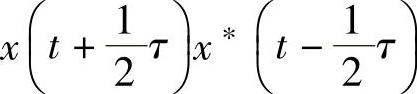
被积函数称为魏格纳自相关函数。从其内积形式可以看出，WVD是对x（t）局部化。
WVD是一种重要的二次（或双线性）时频分布（即信号x（t）在变换中被使用了两次），具有高分辨率、能量集中性和满足时频边缘特性等许多优良特性。然而，由于WVD采用了双线性变换而非线性变换，因此，对于多分量信号会产生严重的交叉干扰项。为了改进WVD的交叉项问题，国内外许多学者展开了大量的研究，提出了多种方法。这些方法对交叉项的抑制起到了很大作用，但是已经证明，不含交叉干扰项且具有WVD聚集性的时频分布是不存在的。虽然WVD在旋转机械故障诊断中得到了广泛应用，但是交叉干扰项的产生影响了其对非平稳信号的精确分析。
二次型时频分布还包括魏格纳时频谱和小波尺度谱等。信号x（t）的魏格纳时频谱定义为其STFT的模值的二次方，即(www.xing528.com)
信号x（t）的小波尺度谱定义为其连续小波变换的模值的二次方，即
小波尺度谱可看作一个有恒定相对带宽的谱图，能够反映信号的时频信息，已被用于机械设备的故障诊断中。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
