小波变换在智能信息处理中的应用

众所周知，傅里叶分析是把一个信号分解成不同频率的正弦波，因此正弦波是傅里叶变换的基函数^[11]。小波分析是傅里叶分析发展史上一个新的里程碑，是近年来发展起来的一种新的时-频分析方法。与傅里叶变换、窗口傅里叶变换（Gabor变换）相比，小波变换是时间（空间）和频率的局域变换，因而能有效地从信号中提取信息，通过伸缩和平移等运算功能对信号进行多尺度细化分析，解决了傅里叶变换不能解决的许多难题，从而被誉为“数学显微镜”^[12]。

1.小波变换的定义

小波变换是一种线性信号处理技术，在小波变换中是用一簇函数去表示信号，这簇函数系称为小波函数系，它是通过如下方法构造的：先选择适当的基本小波ψ（t），然后通过展缩和平移来生成“小波”，即

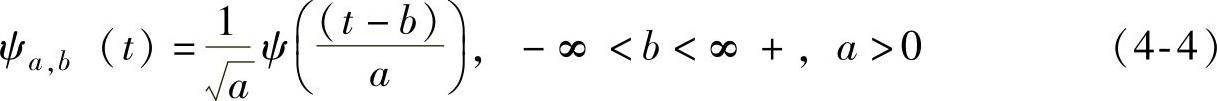
式中ψ（t）称为小波母函数或小波函数，ψ_a，b（t）称为小波基函数。其中，a为展缩参数，b为平移参数。一般地，小波变换的定义为

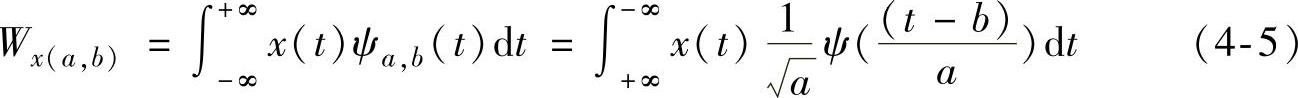
设R表示实数集合，表示平方可积的信号空间，函数L²（R）具有有限能量。对于在函数簇上的分解，这一分解的前提条件是小波函数ψ（t）应满足如下可容性条件：

2.常用的小波变换函数

一般地，在小波变换中，常用的函数有以下几种，如图4-3所示。

（1）Haar小波

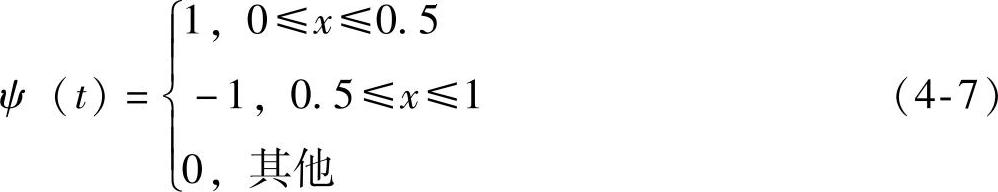
（2）Morlet小波

（3）巴布小波^[13]

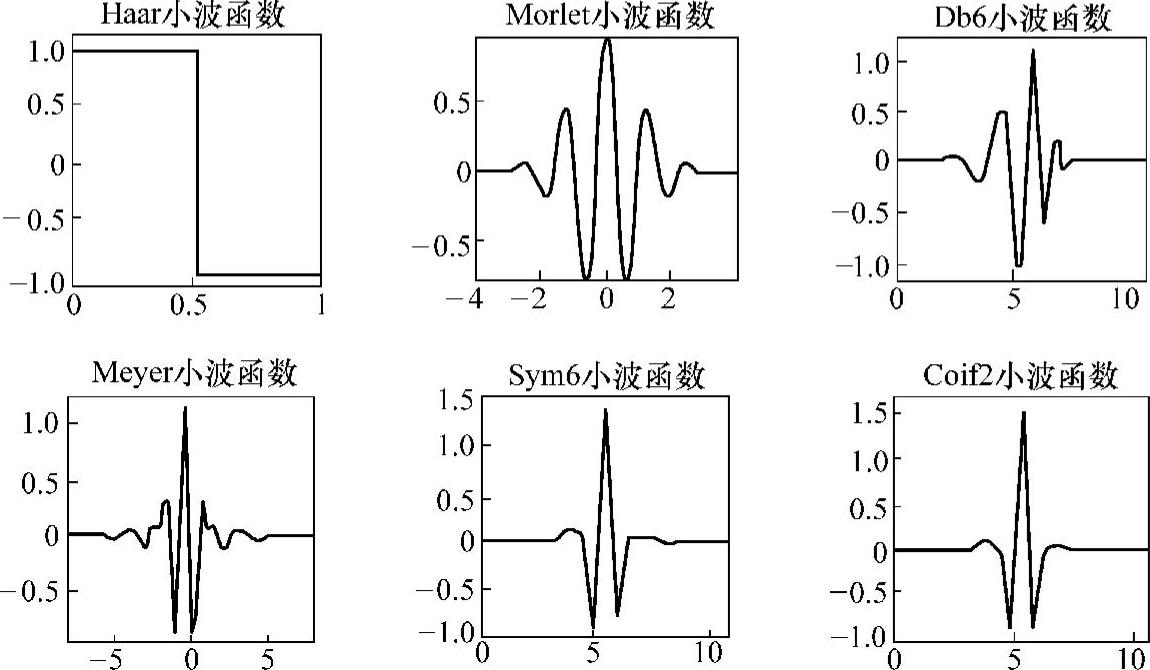
图4-3 小波函数

3.基本小波的选择

基本小波的选择对于小波分析有着重大的影响，对基本小波的选取主要考虑以下几个因素：支撑长度、对称性、消失矩阶数、正则性、正交性。

综合考虑，进行去噪时选择离散二阶双正交小波，它具有线性相位，牺牲正交性的条件下，获得了良好的紧支撑性和精确的对称性，称为对偶的两个小波分别应用于信号的分解与重构中，其中分解小波系数少，有较高的消失矩，对数据有较高的压缩能力，而重构对偶小波系数多，具有较好的正则性，对数据重构的精确度高。

在进行时频分析时，选用Harr小波，Harr小波是一个具有紧支撑的正交小波，该小波不具有消失矩，时域分辨率高，且变换形式简单，易于实现，计算速度快^[4]。

4.小波变换的特点

传统的信号处理方法在处理短时低能量的瞬变信号时，经过滤波器的平滑，不仅信噪比得不到较大的改善，而且信号的位置信息也被模糊掉了，而有些瞬变点的位置是进行分析最重要的信息，小波变换在频域和时域同时具有局部性，能将各种交织在一起的不同频率组成的混合信号分解成不同频率的信号块有利于提取函数的某些本质特征，是一种较有效剔除其他信号和噪声的干扰，从而提高信噪比的手段超声波传感器得到的回波信号大都为时频有限的非稳态信号，在去噪的同时，小波分析可以保留不规则的突变部分^[4]。

而在数据预处理过程中，小波变换是一种很好的有损压缩，但是却是一种“不失真”的压缩，即压缩后的数据和压缩前的数据只是在空间占有量、数据挖掘质量方面有了很大的改进，而数据中隐含的“知识”却不会减少。因为，数据在某些特性上存在着于信号相似的地方，例如，对于连续信号来讲我们可以通过采用香农第一定理来对信号进行不失真“压缩”，同样，对于数据而言，有时候我们无需通过处理大批数据而获得某些知识，我们只要处理这些数据中的部分数据也可以取得同样的效果。小波变换首先作为一种信号处理技术已经发展的比较成熟，将这种理论很好的应用于数据预处理中的数据压缩是很有发展的。特别地，小波变换对于稀疏或倾斜数据以及具有有序属性的数据有很好的压缩效果^[13]。下面分别介绍小波变换在信号处理和数据与处理中的应用。(www.xing528.com)

5.应用小波分析进行信号预处理

在机械设备的振动故障诊断中，通常都需要对信号进行处理，提取特征信号。然而在取得的信号中往往存在各种干扰，如邻近机器或部件的振动干扰、电气干扰以及测试仪器本身在信号传输中的噪声干扰等，这就给故障信号的提取带来了很大的困难，信号中的故障信息常淹没于噪声之中。数据处理的目的在于提高数据的可靠性和数据分析的精度，使故障诊断的灵敏度和可靠性得以提高。信号预处理的核心是采用各种滤波技术提高信噪比，做到去芜存菁，去伪存真。与传统方法相比，小波分析由于可以在时间-频率域对信号进行多层分解，更容易识别出噪声信号。

（1）应用小波分析提取或去除信号中的趋势项

在信号分析中，一般把周期大于记录长度的频率成分叫做趋势项，它代表数据缓慢变化的趋势。这种变化可由于环境条件变化或仪器性能漂移而造成，也可由被监测机器性能的不稳定造成。如果是前者就希望从数据中去除趋势项；如果是后者，由于它包含着机器状态的信息就希望提取趋势项用于诊断。通常趋势项可用下面的多项式给出：

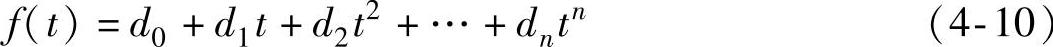
传统的提取或去除趋势项用建立在多项式拟合基础上的简单整系数滤波器来实现。这种方法适合于趋势项随时间作线性增长或按二次方关系增长的情形。一般情况下，多项式的最高拟合指数n＜4，对于其他形式的趋势项则效果不是很好。在小波变换尺度图中，分解尺度的大小反映了信号频率成分的高低，尺度越大，分解信号频率越低。对于信号中的趋势项，因其记录长度一般比较长，对应于小波尺度图中尺度最大或较大的逼近信号。根据具体的实验情况就可以判明其是否需要去除或提取趋势项。在信号的采集过程中，由于测试仪器和被测装置的影响，也常常会引入交流电信号或其他明显的干扰信号，其趋势一般比较和缓，同样也可以用小波分析将其滤除。

（2）应用小波分析进行信噪分离

在对噪声的处理中，一般都把它当作白噪声来处理。白噪声是一个均值为零、功率谱密度在整个频率轴上有非零常数的平稳随机过程。常遇到的高斯白噪声是指具有高斯分布规律的白噪声。传统的去噪方法（如时域平均、相关检测等）通常是针对平稳随机信号而言的，在有用信号和噪声的频谱相互分离时具有良好的效果，但是当有用信号和噪声的频谱相互重叠时，则无法将它们区分开。例如，在齿轮的故障诊断中，常常伴随有冲击信号，冲击信号（突变信号）和噪声信号都具有相当宽的频谱，它们的频谱分量互相重叠，在频域中无法将它们分开。而在时域中，突变信号和噪声信号具有明显的区别。小波分析则结合了时域和频域的优点，根据突变信号和噪声在小波分解尺度图上的不同规律，可以有效地进行信噪分离，而不损失信号的有用信息。

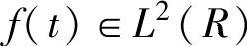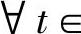
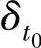由于小波变换对信号的奇异点非常敏感，因而对突变信号的分析非常有效。信号的局部奇异点特性可以用奇异指数来度量。设，若有

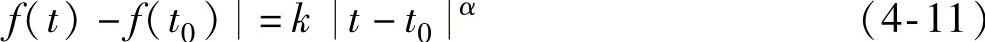
其中k为常数，则称f（t）在t₀处奇异指数为α。函数越光滑，它的奇异指数越大。可以证明：对于一般信号而言，有正的奇异指数，冲击信号具有负的奇异指数，白噪声是一个几乎处处奇异的随机分布，且具有负的奇异指数α=-1/2-ξ，∀ξ＞0。

若小波函数ψ（t）是实的且连续可微，并且具有n阶消失矩（n为正整数）δ_t0为t₀的任一开邻域。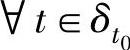，f（t₀）在t₀处具有奇异指数α等价于下述条件成立：

在尺度s下，若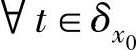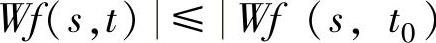，成立，则x₀成为模极大值点。对于上式两边取对数得

从上式可以看出，对于一般信号，由于其奇异指数大于零，随着尺度j的增加模极大值的对数也变大。对于冲击信号和白噪声，由于其奇异指数小于零，其模极大值的对数随尺度的增大而急剧减小。

在小波分解尺度图上，突变信号的幅值一般较白噪声的幅值大。而对于白噪声，尺度减小时，白噪声的小波变换极大模值的幅度急剧增加，其平均稠密度越来越密。因此，根据一般信号、突变信号、白噪声在小波变换下的不同规律，可以通过在小波分解的不同层次上设置一定的阈值，阈值以下的小波系数的模极大值可以认为是由噪声引起的，将其去除，所剩下的则代表了一般信号和突变信号，实现了信噪分离^[12]。

6.小波变换在数据预处理中的应用

在数据信号处理过程中，离散小波变换可以将一个数据向量D转换为另一个数据向量D′（为小波相关系数），且两个向量具有相同长度。但是对后者而言，可以被舍弃其中的一些小波相关系数；如保留所有大于用户指定阈值的小波系数，而将其他小波系数置为0，以帮助提高数据处理的运算效率。这一技术方法可以在保留数据主要特征情况下除去数据中的噪声，因此该方法可以有效地进行数据清洗。此外给定一组小波相关系数，利用离散小波变换的逆运算还可以近似恢复原来的数据。应用离散小波变换进行数据转换时，通常采用一种分层的金字塔算法，该算法在每次迭代中将数据减半，以获得更快的运算性能。该算法主要步骤说明如下：

第一步：输入数据向量的长度L必须是2的整数次幂，因此如果有必要的话需用0补齐数据向量以确保向量长度满足要求；

第二步：每次变换时使用两个函数，第一个负责进行数据的平滑，主要是对噪声数据进行处理，而第二个则负责加权差分计算以获得数据的主要特征；

第三步：将数据向量一分为二，得到两个向量长度为L/2的数据集，然后分别应用第二步中两个函数分别处理这两个数据集，通常情况下这两部分数据分别代表平滑后数据的低频部分和高频部分；

第四步：对由第三步得到的两个数据向量循环使用该步骤中的处理方式，直到所有划分的子数据向量长度均为2为止；

第五步：取出第三步、第四步处理结果便获得了被转换数据向量的小波相关系数^[13]。