智能信息处理技术：数据剔点

由于各种不确定因素导致传感器采集的信号含有不确定成分，在进行A-D量化采样时会夹杂A-D噪声。因此，信号分析前需要对信号进行预处理，即在保持需求信号特征的基础上，尽量消除干扰成分。设计过程中主要采用的方法是剔点处理，以删除过大或过小的毛刺点并加入合适的插值点^[2]。在统计学上已有多种错点剔除方法，如肖维勒准则、狄克逊准则、格拉布斯准则和拉依达准则。

1.肖维勒准则

假设测量得到的n个数据满足正态分布，如果某个测量值X_d（1≤d≤n）的残差满足：C_d＞Z_cσ_x，其中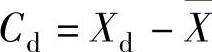，则X_d被视为异常数据，予以剔除。σ_x为标准差，Z_c为肖维勒准则系数，部分值可查表4-1。

表4-1 肖维勒准则系数

2.狄克逊准则

狄克逊准则是通过极差比判定和剔除异常数据，与一般比较简单极差的方法不同，该准则为了提高判断效率，对不同的实验量测定数据应用不同的极差比进行计算。该准则认为异常数据应该是最大数据和最小数据，因此该基本方法是将数据按大小排队，检验最大数据和最小数据是否是异常数据。具体做法如下：将实验数据X_i值的大小排成顺序统计量，X₁≤X₂≤X₃…≤X_n构建不同范围的极差比γ，见表4-2。

表4-2 不同范围的极差比γ

选定显著性水平α，求得临界值D（α，n），见表4-3。若γ_ij＞γ′_ij，γ_ij>D（α，n），则判定X₁为异常值予以剔除。

表4-3 狄克逊准则系数D（α，n）

3.格拉布斯准则(www.xing528.com)

对于服从正态分布的实验数据，将实验数据按值的大小排成顺序统计量：X₁≤X₂≤X₃…≤X_n，格拉布斯导出了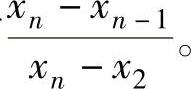

1)选定危险率α。α是采用格拉布斯法判定异常数据出现误判的几率，如1%，2.5%，5%。

2）计算T值如果X_n是可疑数据，则令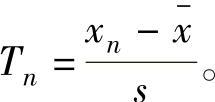

3）根据n及α，查表4-4得到T₀（n，α）值。

4）如果T≥T₀（n，α），则所怀疑的数据是异常数据，应予以剔除。如果T＜T₀（n，α），则所怀疑的数据不是异常数据，不能剔除。采用此法判异常数据产生误判的几率为α。

表4-4 格拉布斯准则系数T₀（n，α）

4.拉依达准则

这种方法是以数据值是否超过标准差σ_x的3倍为判别标准。如果以零均值信号的±3σ_x为置信区间，其置信水平可达到99.74%。通过对错点相邻两点的值求和，再取平均的方法，剔除错点。

假定测试数据满足正太分布的随机信号，则有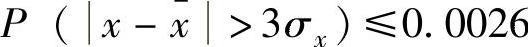。其中，x分别为数字信号的均值和标准差。可见，信号出现大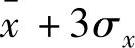于或小于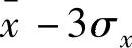的数据概率很小，仅在0.26%以下。因此，可以认为大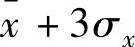于或小于的数据为野点，应予以剔除。

上述的各项准则都有着局限性，如肖维勒准则、格拉布斯准则和狄克逊准则都只能对小样本数字信号进行错点剔除，剔除错点均需查表，对于大样本数字信号则不太适用。拉依达准则可以处理大样本数字信号，但其运算量大，效率不高，而且对幅值有较大变化的信号进行处理的结果比较不理想。针对这个问题，参考文献^[6]提出一种新式的错点剔除准则，能分段对源信号进行处理，在局部剔除错点，处理得更为细致和科学，且能有效地保护幅值较大的峰谷值。对幅值有较大变化的大样本信号，新式错点剔除方法对其错点剔除能取得较为理想的效果。