监测系统中智能信息处理技术-数据采集与信号处理的重要概念

在工农业生产的各个领域中，需要对各种物理参数，例如温度、速度、压力、振动、电压等进行采集、处理和控制，这些参数都是连续变化的物理量，即模拟量。数据采集的任务就是将这些模拟量转换成一组合理的数字量^[2]。下面介绍一些数据采集与信号处理中的一些重要概念。

1.抽样

模拟信号通常是在时间上连续的信号。在一系列离散点上，对这种信号的抽样值称为抽样。信号被抽样后，成为抽样信号，它在时间上是离散的，但是在其取值仍然是连续的，所以是离散模拟信号。如图4-1所示。图中m（t）是一个模拟信号。在等时间间隔T上，对它抽取样值，抽样结果是一系列周期性抽样脉冲。

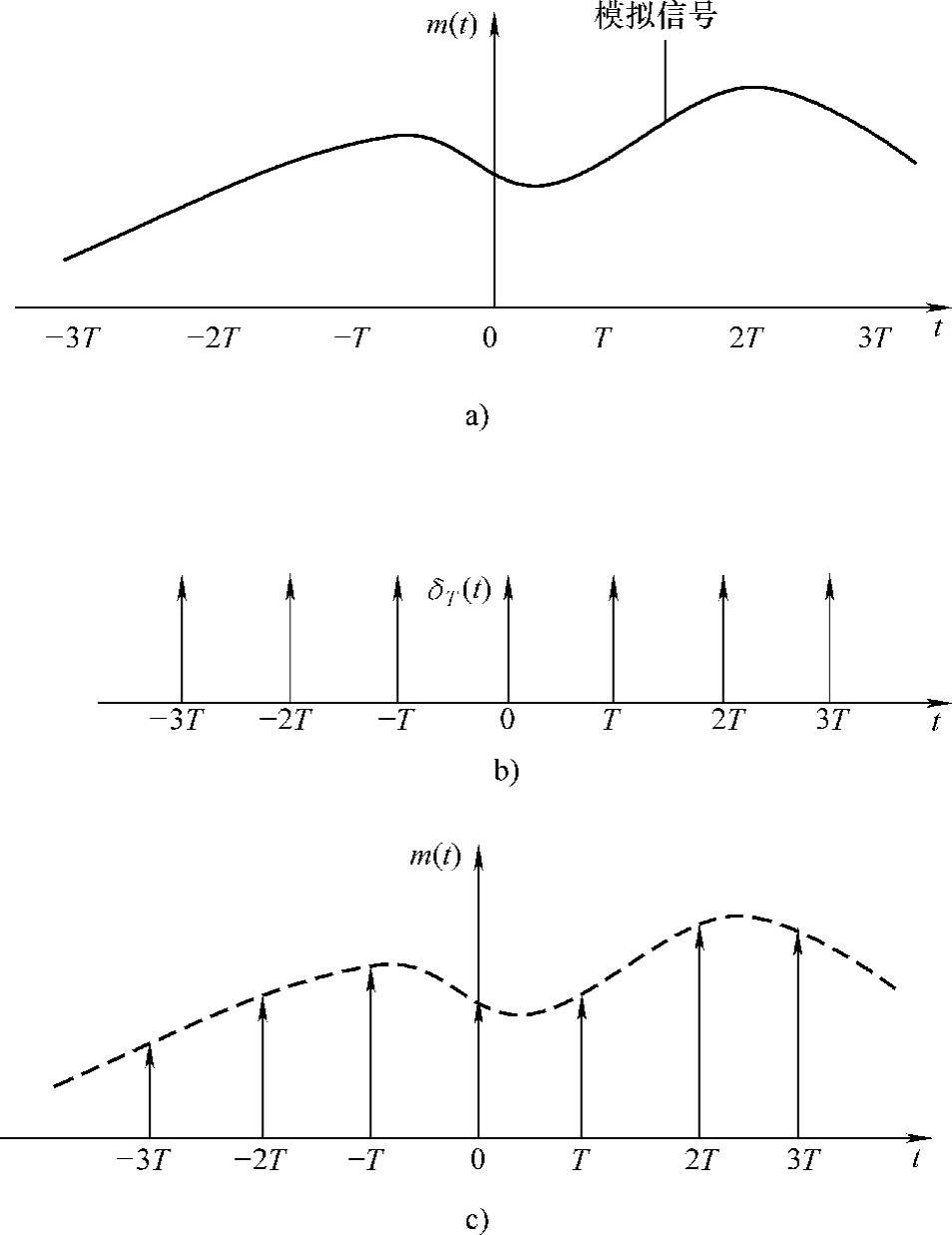
图4-1 抽样信号波形

抽样定理指出：设一个连续模拟信号m(t)中的最高频率小于f_H，则以间隔时间为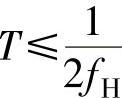的周期性脉冲对它进行抽样时，m（t）将被这些抽样值所完全锁定，这样就能冲抽样信号中恢复原信号。

2.量化(www.xing528.com)

设模拟信号的抽样值为m（kT），其中T是抽样周期，k是整数。此抽样值仍然是一个取值连续的变量。若仅用N个不同的二进制数字码元来代表此抽样值的大小，则N个不同的二进制码元只能代表M=2^N个不同的抽样值。因此，必须将抽样值的范围划分成M个区间，每个区间用一个电平表示。这样，共有M个离散电平，它们称为量化电平。用这M个量化电平表示连续抽样值的方法称为量化。图4-2给出了一个量化过程的例子。图中m（kT）表示模拟信号的抽样值，m_q（kT）表示量化后的量化信号值，q₁，q₂，…q_i，…q₆是量化后信号的6个可能的输出电平，m₁，m₂，…m_i，…m₅为量化区间的端点。这样我们可以写出一般的量化公式：

m_q（kT）=q_i，当m_i-1≤m（kT）≤m_i（4-1）

按照式（4-1）做变换，就可以把模拟抽样信号m（kT）变换成了量化后的离抽样信号，即量化信号。

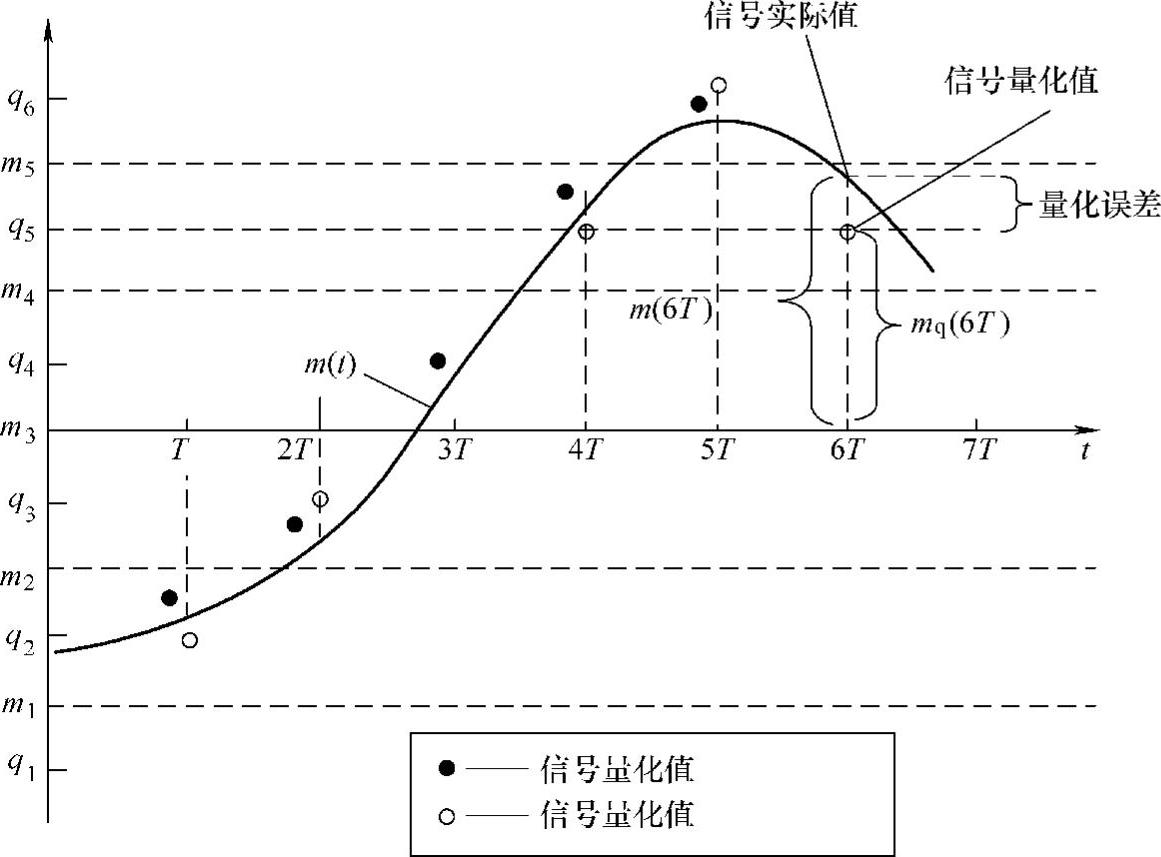
图4-2 量化过程

图4-2中M个抽样值区间是等间隔划分的，称为均匀量化。M个抽样值区间也可以不均匀划分，称为非均匀量化^[3]。