智能信息处理技术在监测系统中的应用

信号是个随时间、空间、或其他某个参量变化的、携带某种信息的物理量。任何可以用确定的数学关系描述的信号，称为确定信号。与确定信号相反，不能用确定的数学关系描述的信号，称为随机信号。以时间为参量的随机信号随时间作无规律的、随机性的变化。这类信号的变化具有随机性，即不确定性。但是随机信号的统计规律却是确定的，所以在数学上，人们用统计学的方法建立了随机信号的数学模型。对于随机信号，信号的统计量起着机器重要的作用。最常用的统计量有一阶统计量，如平均值均值二阶统计量，如相关函数、功率谱密度等。此外还有三阶、四阶等高阶矩、高阶累积量和高阶谱等高阶统计量。随机信号又可分为平稳和非平稳信号两大类。

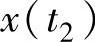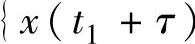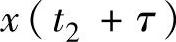若，…的联合分布函数与，…的联合分布函数对所有的t₁，…，t_n和t∈T都相同，则随机过程，称为严格平稳随机信号，也称为狭义平稳。它意味着分布相对于时间移位是不变的。随机信号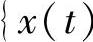，称为广义平稳，如果

1）=m=常数

2）

3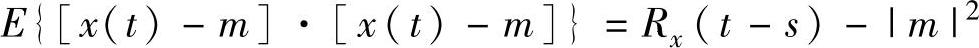），其中R_x（t-s）=

一个严格平稳的随机过程必定是广义平稳的，但一个广义平稳过程不一定是严格平稳的。如果一个信号不是广义平稳的，则称它是非平稳信号。若用统计量叙述，各阶统计量与时间无关的信号称为平稳信号，而某阶统计量随时间改变的信号则称为非平稳信号或时变信号。最常见的非平稳信号是自相关函数或功率谱密度随时间变化的信号。对于确定性信号，当其能量谱不随时间变化时称为平稳信号，反之，称为非平稳信号。因此，我们可以定义非平稳信号泛指具有时变能量谱的确定性信号和具有时变功率谱的随机信号。

监测系统中，从传感器及数据采集系统得到的电流或电压信号，经过A-D转换设备以数字的方式存储在计算机内。监测系统中对信号处理的目的是提取信号的特征，用了描述监测对象的特性。不同种类的信号应采用不同的处理技术。信号的分析和处理是监测系统必不可缺少的步骤。(www.xing528.com)

信号分析和处理技术近些年得到了迅速发展。首先，被监测对象越来越复杂，由具有平稳、线性和周期性特征的对象转变为非平稳、非线性和无统计周期性的对象；其次，信号分析的理论和方法更为先进，如用时频分析代替了频域分析等。

典型的频域分析的方法是傅里叶变换。傅里叶变换的信号频域表示及能量频域分布揭示了信号在频域的特征，但傅里叶变换是一种整体变换，只能了解信号的全局特性，不能有效检测信号频率随时间的变化情况，只有把时域和频域结合起来才能更好地反映非平稳信号的特征。常用的时频分析方法包括线性时频分析法，非线性时频分析法和基于经验模态分解的时频分析法等。

线性时频分析的典型方法有短时傅里叶变换（Short-Time Fourier Transform，STFT）^[23]和小波变换（Wavelet Transform，WT）^[24]。即需要分析的信号含有多个分量时，其时频分布是各子分量的时频分布的线性叠加。其中STFT的基本思想是利用一个窗函数在信号的时间轴上进滑动，并假定信号在窗口内是平稳的。然后计算出信号在各个窗口内的傅里叶变换值，从而得到信号在不同时刻的频谱，取其模的二次方，便得到信号的功率谱。WT和STFT相似，但其时频窗不固定，而是随尺度因子变化。正是由于小波变换方法具有可变的时频窗，使其既能对非平稳信号中的短时高频成分进行定位，又可以对低频成分进行分析。相比较，WT不仅有STFT的优点，而且满足了变窗处理的要求，具有良好的时频局域化特性，与STFT相比，具有更好的时频特性窗口。

非线性时频变换中应用最广泛的是二次双线性时频分布，主要有Winger-Ville分布^[25]和Cohen类双线性时频分布^[26]。有别于线性时频表示，Cohen类双线性时频分布的实质，是将信号的能量（信号的某种平方形式）分布于时频平面内，即采用对信号的双线性乘积进行核函数加权平均的方法来实现的非线性时频表示，它们表示的是信号的能量密度分布，这种表示不满足线性叠加性。

希尔伯特-黄变换（Hilbert-Huang Transform，HHT）^[27]是基于经验模态分解的时频分析方法，它是处理非线性、非平稳信号的较好的一种时频分析方法。它直接由信号本身构造基函数，从局部时间尺度入手，获得不同尺度特征的固有模态函数（IMF）。Hilbert谱的时间和频率分辨率是相互独立的，能获得比小波谱更高的时间和频率分辨率，因此该方法具有良好的局部适应性和结果的直观性。