 任务情景
任务情景
我们都是采用十进制数来表示数据,而计算机中的电子设备,只有开关或电平高低两种状态,那计算机如果来表示数据呢?小明带领他的学生去了解计算机中数据的表示。
 任务分析
任务分析
◆数制的概念
◆不同数制之间的相互转换
◆计算机中信息的表示
 知识准备
知识准备
1.进位计数制
进位计数制,简称为数制或进制,是利用固定的数字符号和统一的规则来计数的方法。计算机是由逻辑电路组成,逻辑电路通常只有两个状态,开关的接通与断开,这两种状态可以用“0”和“1”表示,而二进制数也只有两个数符“0”和“1”,并且二进制数计算规则简单,并适合做逻辑运算,从第一台“冯·诺依曼”计算机到现在,计算机内都使用二进制数对数据进行存储、加工、处理。人们最熟悉的是十进制数,所以在计算机终端都设计为能够接收十制数的输入和输出。另外,为方便理解和读写,在输入输出的时候还可以使用八进制数和十六进制数。
1)十进制数(Decimal)
十进制数的每个数位有可以有0、1、2、3、4、5、6、7、8、9共10个不同的数符表示,每一个数位上所代表的数值也不相同。如十进制数345.2,其中3代表的值为3×100,4代表的值为4×10,5代表的值为5×1,2代表的值为2×0.1。这里的100、10、1、0.1为每个数位上数×的固定值,这个固定值与它位置的关系为10i,其中i=n-1,n-2…,1,0,-1,…-m,这个固定值称为位权。则345.2“按权展开”为
![]()
对于任意十进制数可按权展开为:
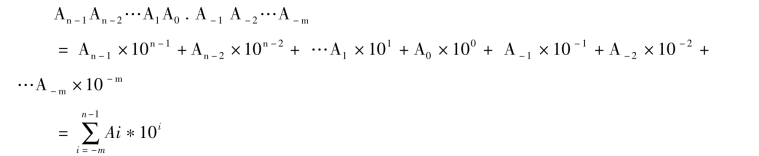
作为任意R进制数包括以下基本概念:
(1)基数。R进制所包含的数符个数。十进制数的基数为10。
(2)数符。R进制计数的符号。十进制数的数符有0、1、2、3、4、5、6、7、8、9。
(3)权。也称位权,R进制的数据在相应位上1所表示数值的大小。十进制数的位权为10i,其中i是数据所在的位置,小数点前一位为0,往前依次加1,往后依次减1。
(4)计数规则。R进制的进位和借位的规则。十进制数的计数规划为逢十进一、借一当十。
对于任意R进制数可按权展开为:

2)二进制数(Binary)
(1)基数。二进制数的基数为2。
(2)数符。二进制数的数符有0、1共2个。
(3)权。二进制数的位权为2i。
(4)计数规则。二进制数的计数规划为逢二进一、借一当二。
对于任意二进制数可按权展开为:
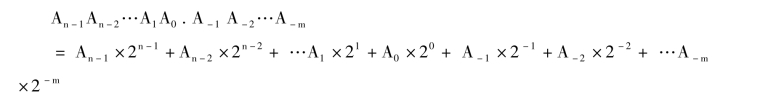
如:二进制数1101.1按权展开为
![]()
3)八进制数(Octal)
(1)基数。八进制数的基数为8。
(2)数符。八进制数的数符有0、1、2、3、4、5、6、7共8个。
(3)权。八进制数的位权为8i。
(4)计数规则。八进制数的计数规划为逢八进一、借一当八。
对于任意八进制数可按权展开为:
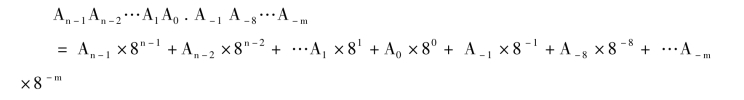
如:八进制数327.6按权展开为
![]()
4)十六进制数(Hexadecimal)
(1)基数。十六进制数的基数为16。(https://www.xing528.com)
(2)数符。十六进制数的数符有0、1、2、3、4、5、6、7、8、9、A、B、C、D、E、F共16个,其中A—F分别表示10—15。
(3)权。十六进制数的位权为16i。
(4)计数规则。十六进制数的计数规划为逢十六进一、借一当十六。
对于任意十六进制数可按权展开为:
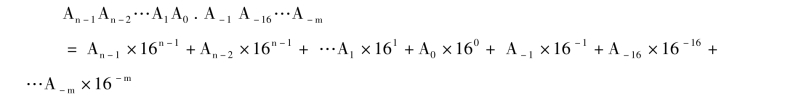
如:十六进制数A2D.6按权展开为
![]()
为了区别不同的数制,在表示时候可以采用两种方法,一种是把数用圆括号括起来,在右下角数数字标注,如(345.2)10,(1101.1)2,(327)8,(A2D)16,另一种是用后缀字母来表示,十进制的后缀字母为,二进制的后缀字母为B,八进制的后缀字母为O,十六进制的后缀字母为H,如345.2D,1101.1B,327O,A2DH。当数值即没有下标标识,也没有后缀字母标识的时候默认为十进制数,如101为十进制数。
2.不同进制之间的相互转换
1)其他进制转换为十进制数
其他进制转换为十进制数的时候就用按权展开求和的方式。
【例1-3-1】把二进制数101011.01B转换为十进制数

八进制和十六进制转换成十进制的方法相同,在此略过。
2)十进制数转换为其他进制
将十进制数转换为其他进制时,需将整数和小数分开,分别转换成R进制再拼接起来,转换后小数点位置不变。其方法是:整数部分:除以R取余数,直到商为0,得到的余数即为R进制数各位的数码。小数部分:乘以R取整数,得到的整数即为R进制数各位的数码。
下面以十进制转换为二进制为例来说明转换过程。
【例1-3-2】把十进制整数217.375转换成二进制数。
整数部分转换(除2取余倒排)小数部分转换(乘2取整顺排)

把整数部分和小数部分转换的结果拼接起来就得到十进制整数217.375转换成二进制数的结果
(217.375)10=(11011001.0.011)2
试试把217.375转换成八进制数和十六进制数。具体方法同上,在此略过。
3)二进制与八进制、十六进制之间的相互转换
八进制和十六进制都是为了方便理解和读写二进制数而有的,其中1位八进制数对应3位二进制数,这样就可以把二进制数缩短3倍左右;而1位十六进制数对应4位二进制数,这样就可以把二进制数缩短4倍。
(1)二进制转换为八进制,只要将二进制数从小数点开始,整数部分从右向左3位一组,小数部分从左向右3位一组(不足3位补零),把每组的3位二进制数按权展开求和,相对位置不就,即可完成转换。
【例1-3-3】把二进制数(10110101.0011)2转换成八进制数。

(2)八进制数转换成二进制数,是上述方法的逆过程,把每1位八进制数转换为3位二进制数,小数点位置和数据的相对位置均不变。
【例1-2-4】把八进制数(107.23)8转换为二进制数。

二进制与十六进制之间的转换和二进制与八进制之间的转换类似,只是4位一组。
【例1-2-5】把二进制(111010100001010)2转十六进制
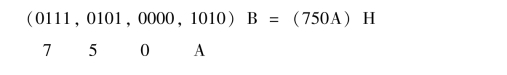
 任务实施
任务实施
1)下面的数据表示哪些是错误的,为什么?
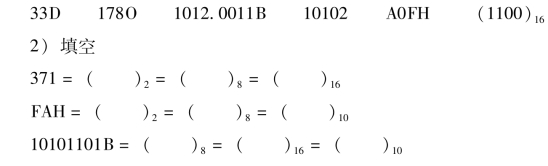
为了方便我们在十进制、二进制、八进制和十六进制之间进行转换,表1-3-1列出了0~15十进制数与二进制数、八进制数和十六进制数之间的对应关系。
表1-3-1 二进制数、八进制数、十六进制数与十进制数值的对应关系

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。




