敏感性分析：水利与国民经济协调发展的研究成果

敏感性分析的目标是为了研究水利投资在占GDP不同比重的情况下，模型的目标值GKP的变化情况，进而分析其中的定量变化规律。可以通过限定水利投资的范围，求出不同水利总投资规模下，宏观经济和水利损失变化情况，分析最优方案的敏感性。

为了对模型的敏感性进行分析，设定以下方案集进行计算分析。为便于比较，对方案1的投资区间进行适当调整，即投资比例介于0.85%～0.95%之间，如表6.14所示。

表6.13　方案1和方案2对比分析水利投资的效益分析

表6.14　敏感性分析计算方案集　单位：%

通过计算，可以得到不同方案的各种损失以及GKP 值，分别见表6.15 和表6.16。

表6.15　不同方案水平年的总损失值　单位：亿元

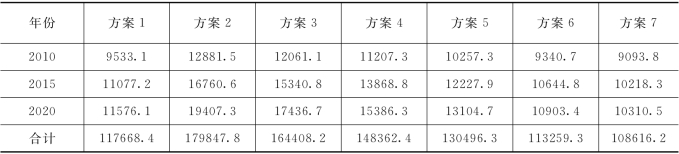
表6.16　不同方案水平年的GKP　单位：亿元

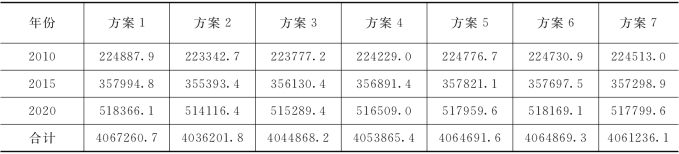
从总量来分析，可以看到不同投资比例区间对宏观经济和水利损失变化情况，如图6.11、图6.12所示。

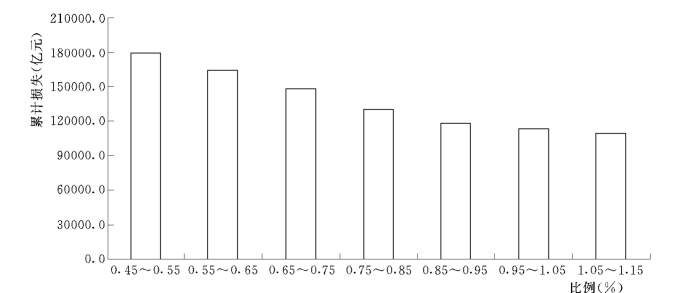
图6.11　水利投资对各项水利损失的影响(www.xing528.com)

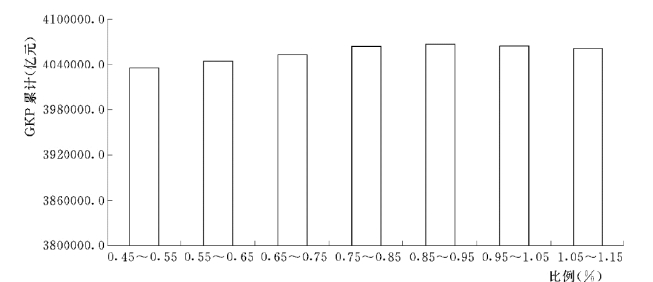
图6.12　水利投资对GKP的影响

由敏感分析可以看出，模型结果符合基本规律：随着水利投资的增大，水利的损失值逐渐减少，调整后的GKP在最优区间（水利投资在占GDP0.85%～0.95%之间时）达到最大，即此时的水利与国民经济处于最佳的协调发展状态，这种定量分析得出的规律正是本章开始部分关于水利与国民经济相互作用关系基本理论的体现。

另外，以最低投资方案（方案2）为对比标准，分析各个方案的GKP增加部分和投资增加部分的比值，可以得到各个方案相对于方案2的投资增加部分的效益，计算结果如表6.17、表6.18和表6.19 所示。

表6.17　各个方案相对于方案2的投资增加量　单位：亿元

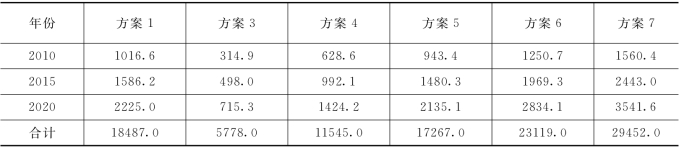
表6.18　各个方案相对于方案2的GKP增加量　单位：亿元

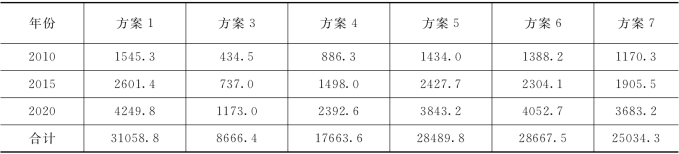
从增加的效益变化可以看出，在最低投资比例（方案2 的0.45%～0.55%）和最佳投资比例（方案1 的0.85%～0.95%）之间，随着投资比例的增加，增加部分的投资效益不断增大，说明增加投资比例是合理的，而达到最佳投资比例以后，再增加投资，整个投资增加部分的效益呈下降趋势。方案1 的目标函数GKP明显优于其他方案。

表6.19　各个方案相对于方案2的投资增加效益变化　单位：%

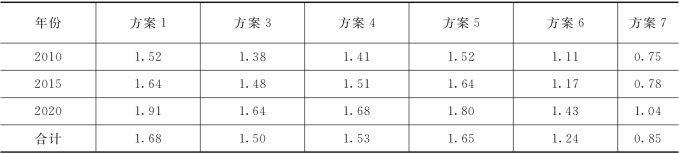
通过整体核算模型的计算和分析，可以看出水利投资与国民经济发展之间的动态联系，由此得到的未来水利投资的合理区间，可以作为水利与国民经济协调发展的重要调控指标。