局部闭模型技术：水利与国民经济协调发展研究成果

投入产出局部闭模型技术是Wassily W.Leontief教授提出来的。经济模型按照与外部环境的关系可分为开模型和闭模型两种。开模型中一部分变量是外生变量，其数值是给定的。闭模型中所有变量都是内生变量，都是在模型求解过程中确定其数值的。在静态投入产出模型中：

通常认为最终需求Y，即消费、投资、进出口等的数值是给定的，是外生变量，而各部门产量X 是通过模型求解得到的，是内生变量。这个模型通常称为投入产出开模型。

在分析水利投资的总量和结构效应的时候，应该考虑到居民收入的增加以及消费的扩大所带来的直接和间接影响。为此，采用局部闭模型的技术来分析水利投资对产出和就业所带来的影响。采用局部闭模型时将居民看作一个部门加入到中间流量矩阵，即在投入产出表第一象限增加劳动者报酬行向量和居民消费列向量，使第一象限由n阶方阵扩展为n＋1 阶方阵。这一分析技术的优点在于在局部闭模型中通过计算逆矩阵可以包括开模型所未包括的如下重要间接影响，即：由于水利投资的增加，使得劳动者报酬增加，从而扩大了消费，又进一步拉动各部门生产的发展。这样，水利投资的直接消耗和间接消耗才能全面反映出来，经济意义上更加合理。这样来分析水利投资对国民经济的影响才更全面。

在投入产出局部闭模型中，把居民作为一个部门列入第Ⅰ象限。居民部门的行是以货币形式表现的各部门支付的劳动报酬；居民部门的列是居民对各种消费品和劳务的消费额。由此得到扩展的直接消耗系数矩阵A*：(www.xing528.com)

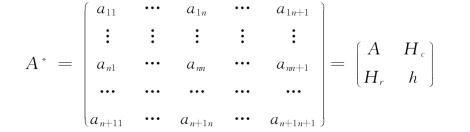
式中：Hr为各部门劳动报酬系数行向量；Hc为居民收入对各部门产品和劳务的直接消耗系数列向量；h 为居民对居民的支付系数。

在扩展的A*矩阵基础上计算扩展的完全需要系数矩阵（I－A*）－1，即局部闭逆。它与通常的完全需要系数矩阵（I－A）－1的区别是，（I－A）－1只反映通过中间投入引起的对各部门产出的直接和间接需要，而（I－A*）－1不仅反映通过中间投入而引起的各种直接和间接需要，而且反映由于居民劳动报酬增加，居民消费需求增加而引起的对各部门产出的直接和间接需要（见图5.2，图中虚线表示通过居民部门而传递的影响）。