实现RGB-D行为识别的双流Siamese网络方法

1.3D CNN结构

本节多源视觉数据是RGB和Depth图像序列（视频），所以选取3D CNN作为C2s-S3DCNN的基础网络结构，由六个卷积层组成：两个最大池化层，两个GAP层以及一个FC层，如图4-27所示。在将训练视频输入到3D CNN之前，需要对训练视频采取随机抽样、裁剪、color jittering等图像处理技术，得到空间尺度为112和时间长度为32的训练视频。因此，对于3D CNN的输入，每个RGB视频的大小为3×32×112×112，而每个深度视频的大小为1×32×112×112。接下来，以RGB模态数据为例，分别对网络结构中的卷积层、池化层、GAP层、FC层及其参数进行介绍。

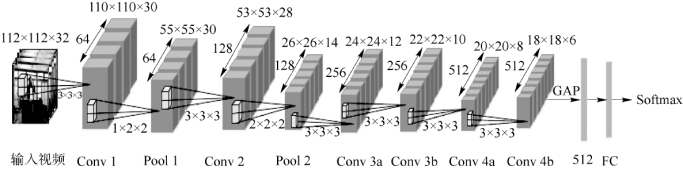
图4-27　3D卷积神经网络结构

（1）3D卷积层：3D CNN结构中有六个卷积层，每个卷积层中卷积核的个数分别为64，、128、256、256、512、512，卷积核的大小为3×3×3，每个卷积核的步长都为1×1×1。此外，为了加速网络的训练过程和减少初始化的影响，参照Conv LSTM在每个卷积层（除了Conv3a和Conv4a层）的后面使用批归一化处理（BN）以及激活函数（Re LU）。

（2）3D池化层：在3D CNN中，只在第一和第二个卷积层后加入池化层。同时为了保留初始卷积层中的时间信息，在第一个池化层进行空间池化，而在第二个池化层进行空间和时间池化。因此，第一个池化核的大小和步长均为1×2×2，第二个池化核的大小和步长均为2×2×2。

GAP层以及FC层：为了减少网络参数和避免过拟合问题，在Conv4b后用GAP层代替原始的全连接层。需要说明的是GAP层的池化是在每一个3D特征图的空间维度和时间维度进行整体平均池化，因此，GAP层的输出是一个长度为512的特征向量。该特征向量最后输入到一个带有Softmax的FC层。

2.中心对比损失函数

对比损失函数是Siamese CNN的重要组成部分。其主要目的是使得网络能够减少正样本对之间的特征变化，而增加负样本对之间的特征差异。本小节结合对比损失函数和中心损失函数的思想，设计了两种中心对比损失函数：模态内中心对比损失函数和异质模态中心对比损失函数。其中模态内中心对比损失函数使得RGB或深度模态下的样本特征具有更小的类内变化和更大类间差异；同时跨模态中心对比损失函数使得RGB和深度模态下的样本特征具有更小的类内变化和更大类间差异。下面对以上两种中心对比损失函数的设计细节进行详细介绍。

（1）模态内中心对比损失函数

图4-28给出了本节所涉及的几种对比损失函数的对比。如图4-28（a）所示，原始的对比损失函数需要对所有的样本数据进行相似/不相似关系度量，以使得同一个类别的样本数据（图中的三角形或圆圈）彼此靠近，而使得不同类别的样本数据（图中的三角形和圆圈）彼此疏远。这种方式的缺点在于对所有的样本数据都进行关系度量，从而产生大量的计算成本和训练时间。Berlemont等人在引入类参照样本的基础上，提出在每个类别的参照样本与剩余所有样本之间作相似与不相似度量，即图4-28（b）中的白色三角形、圆圈与灰色的三角形、圆圈。这种方式同样也会产生一些冗余的计算，因为样本数据的欧式距离关系具有传递性，当某个样本与其类别参照样本的距离比较小，而参照样本与另一个类别的参照样本具有较大距离时，该样本与另一个类别的参照样本也有较大距离。因此，此时就不需要再对该样本与另一个类别的参照样本进行欧式距离度量计算。基于上述观察动机，本节介绍一种新的中心对比损失函数，并用于相同模态数据（相同维度）的语义度量。所设计的中心对比损失函数只考虑在相同类别的样本数据和参照样本的数据之间作相似度量，即图4-28（c）中的三角形或圆圈；而在不同类别的参照样本数据之间做不相似度量，即图4-28（c）中相同颜色的三角形和圆圈。

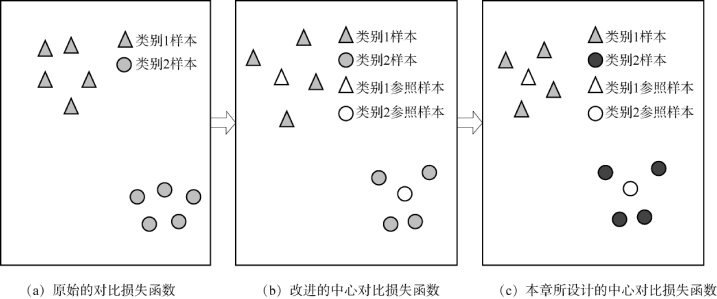
图4-28　几种对比损失函数的对比

根据上述观察动机和公式（4-82），对于RGB模态数据本节所设计的中心对比损失函数可表示成如下公式：(www.xing528.com)

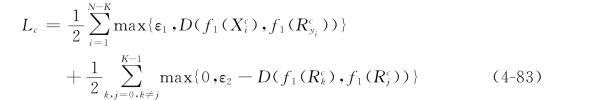
式中，0≤ε1，ε2为自定义的阈值参数，且有ε1≪ε2；f1（X）表示RGB模态下的样本X在3D CNN中GAP层输出的特征向量，D（f1（X），f1（R））=‖f1（X）-f1（R）‖2表示f1（X）与f1（R）的欧式距离。从公式（4-83）中可以看出，最小化目标函数Lc就可以保证RGB模态类内样本之间的靠近及不同类样本的分离。同样的方式也可以得到深度模态中心对比损失函数的定义：

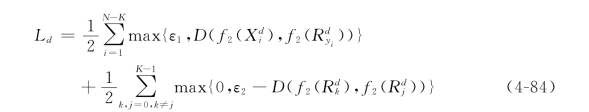
式中，ε1，ε2的定义如上所述，f2（X）表示深度模态下样本X在3D CNN中GAP层输出的特征向量。最后，Lc和Ld就构成本章的模态内中心对比损失函数。

（2）异质模态中心对比损失函数

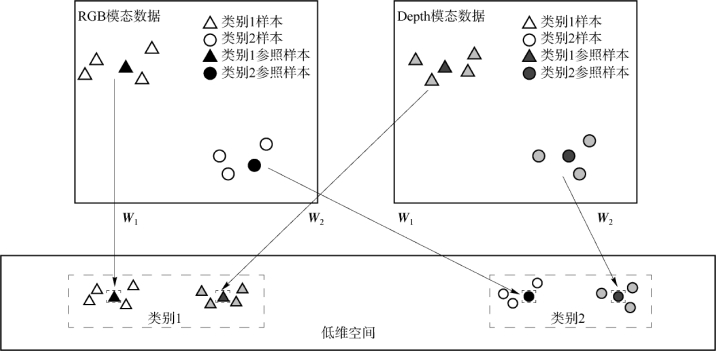
图4-29　RGB和Depth模态下两个类别样本的相似与不相似度量

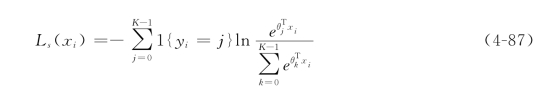
式中，yi为样本的类别标签，1{yi=j}为指示函数，当yi=j时函数值为1，否则为0。最后，结合公式（4-83）、公式（4-84）、公式（4-86）、公式（4-87）就可以得到整个网络的损失函数为

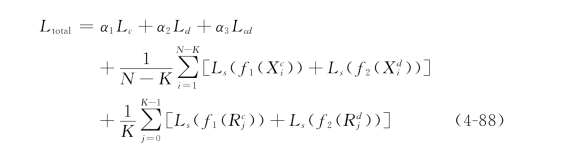
式中，α1，α2，α3为三个中心对比损失函数的平衡参数。在公式（4-88）中，Softmax损失函数有两种：RGB模态数据的Softmax损失和Depth模态数据的Softmax损失。在这两种Softmax损失函数中，它们的参数θc和θd是不同的。将以上三个中心对比损失函数和Softmax损失函数相结合，就可以使得整个网络能够学习到更加具有区分能力的模态特征，同时减少同一类别内的样本特征在同一个模态（RGB或Depth模态）以及不同模态（RGB和Depth模态）上的数据差异。在得到每个分流网络的Softmax模型参数θc和θd后，对于一个测试视频，通过Product-Score融合方式得到视频的类别标签，即将两个分流网络的输出结果向量进行点乘，并将最终结果向量中最大值的索引作为测试样本的类别标签。