多源视觉信息感知与识别实验结果分析

本节在单一模态（RGB或Depth）图像上和两种不同模态（RGB和Depth）图像上对MSG-DNMF模型进行测试，并将MSG-DNMF算法与主流的多模态特征学习算法进行对比。在单一模态图像上的实验是为了测试在面对相同数据来源、不同类型特征时的联合表达效果。而在两种不同模态的图像上进行实验则是为了测试MSG-DNMF算法在面对不同数据来源时的多模态特征联合表达效果。由于在行为识别过程中，RGB和深度图像具有明显的差异性，导致两种不同数据来源的多模态特征存在高层语义模糊。因此，针对不同模态图像的多模态特征联合表达进行实验更具有现实意义。

如章节4.3.3所述，实验过程中采用平均识别准确率作为指标来定量描述算法的性能。实验的仿真平台为主频4.00 GHz×8的Intel Core i7-6700K CPU，操作系统为Ubuntu 16.04，仿真软件采用MATLAB和Python。在实验过程中，对于MSG-DNMF模型中的参数λ1、λ2、λ3、λ4，采取遍历原则寻找最优模型参数，从而得出本节中所提出的不同正则项对算法性能的影响。而对于其他参数，如：不同模态特征的基本语义概念字典Vm维度大小cm，m=1，…，M，所有模态特征的共享语义字典V的大小d和MSG-DNMF算法的迭代次数T也会在后续实验中做进一步讨论。

此外，本节还主要比较了三种不同类型的多模态特征学习算法：（1）常见基于NMF的多模态特征联合学习算法；（2）基于不同图正则约束的多模态特征联合学习算法；（3）其他多模态特征联合学习算法。

1.不同模态特征的语义概念字典维度对算法性能影响

由于不同模态特征具有不同的特征维度，使得MSG-DNMF模型中相应模态特征数据具有不同的基本语义概念字典维度。在实验过程中将每种模态特征的语义概念字典维度cm，m=1，…，M设为原始特征空间维度dm的{10%，30%，50%，70%}并取整后进行性能评估。图4-22给出了不同的语义概念字典维度大小设置对四个数据库的识别性能影响。从图中可以看出对于每种模态特征，过大或者过小的基本语义概念字典维度都会造成模态信息的丢失，从而影响多模态特征的联合表达效果和最后基于多模态表达的行为识别结果。当cm=0.3dm和cm=0.5dm时，在每个数据集上的平均识别准确率几乎没有太大区别，同时过大的语义概念字典维度会带来较大的计算成本。因此，在实验过程中将每种模态特征所特有的语义概念字典维度设置为原始模态特征维度的30%，即cm=0.3dm。

图4-22　不同模态特征所特有的语义概念字典大小在四个数据库上的识别性能

2.所有模态特征的共享语义概念字典维度对算法性能影响

针对MSG-DNMF算法中共享语义概念字典V的大小d，分别测试了d=[20，40，60，80，100，120，140，160，180，200]十种情况。为了确定该参数的值，将cm的值设为0.3dm以及令λ1、λ2、λ3、λ4的值为1后，在四个不同的数据库上进行测试。图4-23为不同的共享语义概念字典大小在四个数据库上的平均识别率。此外，为了能更好地说明参数对算法的影响，在实验过程中还增加了与一些变形算法的对比测试。其中Double NMF（DNMF）算法仅保留了目标函数（公式（4-53））中的数据分解项，即λ1、λ2、λ3、λ4的值为0；Regularized DNMF（RDNMF），Orthogonal DNMF（ODNMF），Sparse Graph DNMF（GDNMF）则对应着公式（4-53））中的不同正则项，如RDNMF模型中λ1=1，λ2，λ3，λ4=0；GDNMF模型中λ2，λ3=1，λ1，λ4=0；ODNMF中λ1，λ2，λ3=0，λ4=1。(www.xing528.com)

从图4-23可以看出，当d的值达到某个数值后，MSG-DNMF算法及其变形的平均识别率达到了最优。随着后续d值的增加，平均识别率的涨幅不再明显甚至出现下降趋势。同时在所有的共享语义概念字典维度上，MSG-DNMF算法的性能几乎高于DNMF、RDNMF、ODNMF和GDNMF的识别性能。此外，不同的数据库达到最优识别准确率所需的d值也不同，H MDB51和MSR Action3D的最优d值分别为160和120，而MSR Daily Activity3D和SYSU 3DHOI的最优d值为100。上述现象的原因在于数据库H MDB51和MSR Action3D中包含较多的行为类别，从而需要更多的共享语义字典数目来对行为数据进行描述。考虑到维度增加带来的计算成本，实验过程中将HMDB51的d值设为150，而将MSR Action3D、H MDB51和MSR Action3D的d值设为100。

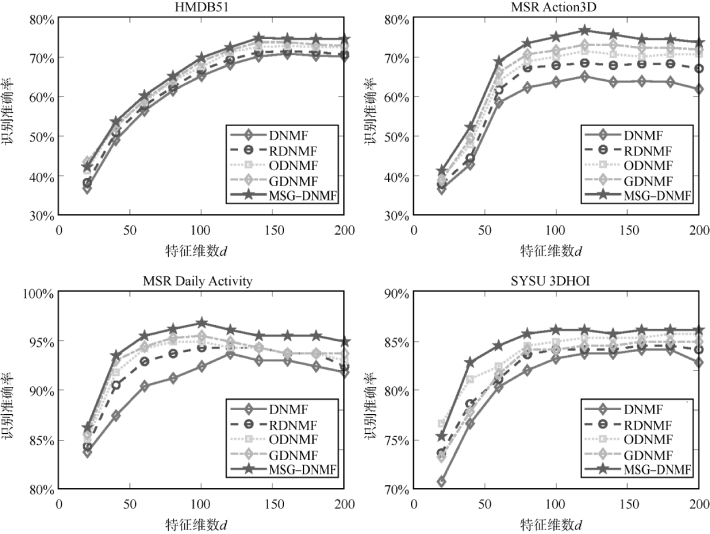
图4-23　MSG-DNMF算法中不同共享语义概念字典维度在四个数据库上的识别性能

3.MSG-DNMF算法的迭代次数与收敛性

对于MSG-DNMF算法的迭代次数，这里分别测试了T在区间[20，1000]上的目标函数值变化。为了确定迭代次数，将其他参数设置为最佳参数值后在四个不同的数据库上进行了测试。不同迭代次数所得到的目标函数值如图4-24所示。实验结果表明，当迭代次数达到200次左右时，在四个数据库上的目标函数值基本达到收敛，即当T≥200后，目标函数值变化随着迭代次数的增加不是很明显。因此，实验过程中将迭代次数T设为200。同时与其他三个数据库相比，由于HMDB51中有较多的训练样本，使得迭代次数小于200时目标函数值具有慢的收敛过程。

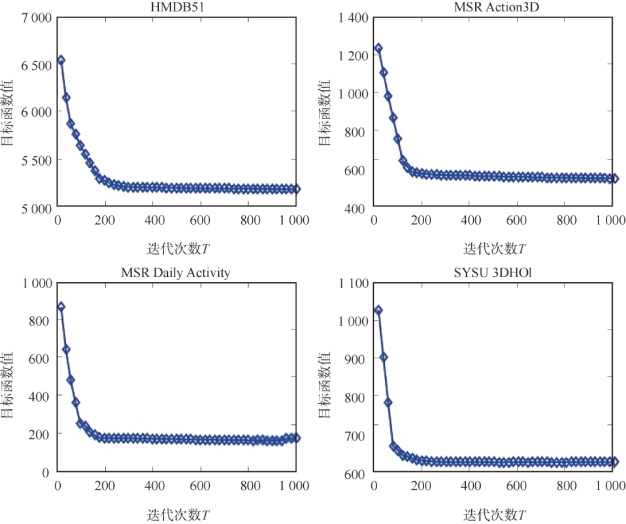
图4-24　MSG-DNMF算法中不同迭代次数在四个数据库上的目标函数值