多源视觉信息感知与识别：实现MSG-DNMF算法

本节介绍基于多模态稀疏图约束的非负矩阵分解算法，记为MSG-DNMF算法，并通过MSG-DNMF算法实现了多模态特征的联合表达。该算法通过研究多模态数据中潜在的几何结构，创新性地将相同模态和不同模态数据下的稀疏图引入到非负矩阵分解的过程中。从非负矩阵分解项和图正则约束项两个方面出发，对现有GNMF算法进行改进。MSGDNMF算法既能学习到多模态数据的共享语义子空间，也能保持样本在原有模态数据上的流形结构，从而有效地解决了现有基于图约束的多模态特征联合表达过程中所存在的问题。

1.多模态联合非负矩阵分解项

虽然不同模态特征数据在表达上有着一定的差异，但是同一类样本的不同模态特征却有着相同的语义概念。因此，研究人员普遍假设各模态原始特征数据之间存在潜在公共因子，然后采取联合矩阵分解技术获得这些模态特征的公共因子。由于对不同的底层视觉特征进行池化和特征量化后得到的各种模态特征数据都是非负的，所以采取NMF算法对各种模态的特征数据X m，m=1，…，M进行非负分解，从而得到这些模态特征数据的共享因子V∈R d×N，d表示分解后得到的共享空间维度。由于每种模态特征数据的特殊性，不能简单地用X m≈P m V来表示整个分解过程。其主要原因在于某些模态特征数据的维度可能比较低，从而在对X m进行聚类过程中可能会得到不同的聚类字典数量，直接将聚类字典数量和系数空间维度约束为相同的数值，可能会引入比较大的误差。改进的多模态非负矩阵三分解模型，目标函数表示如下：

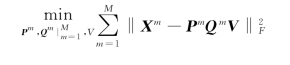
式中，Icm表示cm阶的单位矩阵。对比公式（4-46）和公式（4-47），改进后的目标函数具有以下两个优势：（1）在第一层分解中，可以得到不同模态特征数据所特有的字典系数V m，从而能够对V m进行图正则化约束，使得各模态特征矩阵分解后能够保持原始数据中的几何结构；（2）保证每个模态特征数据的字典矩阵P m更加接近最理想的聚类字典矩阵，也能减少各种模态特征原始数据分解过程中的误差。

2.多模态稀疏图构造

样本数据在多个模态特征空间中存在一些复杂的低维流形嵌套。首先，在每个模态特征空间上，样本之间存在特定的几何结构关系；其次，在两个不同的模态特征空间上，样本之间存在一定的语义关联关系；而就所有模态特征数据而言，样本之间也会存在一种几何结构关系。为了更好地表达和使用这些隐含的结构关系，本节构造了三种不同类型的图结构，即三种图邻接矩阵，以用于后续图正则约束的学习。

定义4.1 邻接矩阵：表示图G=（¯V，E）中顶点¯V={v1，v2，…，vn}之间相邻关系的矩阵A=（aij）n×n，其中对角线上的元素aii=0，i=1，…，n。

对于一个无向图G，其对应的邻接矩阵为对称矩阵即A T=A，图4-19给出了一个无向图结构及其对应的邻接矩阵。每个样本可以看作是一个图的顶点，而样本模态特征数据之间的相似度或语义关系可以看作是两个顶点之间连接权重，从而构造样本数据的邻接矩阵。与热核函数和欧式距离函数相比，稀疏表示方法得到的图邻接矩阵更能反映原始数据中的几何结构。因此，本节选择使用改进的稀疏表达方法构造样本在单一模态数据和两种不同模态数据下的图邻接矩阵。

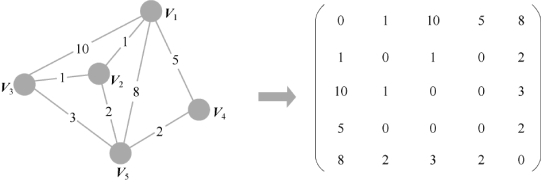
图4-19　图及其对应的邻接矩阵

（1）单一模态数据下的图邻接矩阵构造

对于每种模态的特征数据X m，m=1，…，M，根据稀疏表达方法构造相对应的邻接矩阵A m以及拉普拉斯图矩阵L m，m=1，…，M。由于公式（4-44）中仅仅在稀疏表达的过程中加入稀疏约束，而可能使得相似的特征数据在经过稀疏表达后得到误差较大的表达系数。基于局部约束线性编码（Locality-constrained linear coding，LLC）的思想，本节将样本之间的类别信息代替样本之间的距离信息作为一种局部约束加入稀疏表达过程，从而使得同一类别的样本模态特征具有相似的编码系数。改进后的稀疏表达目标函数如下：

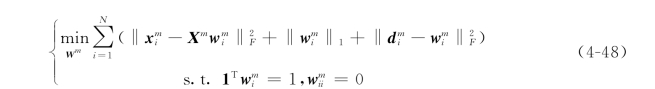
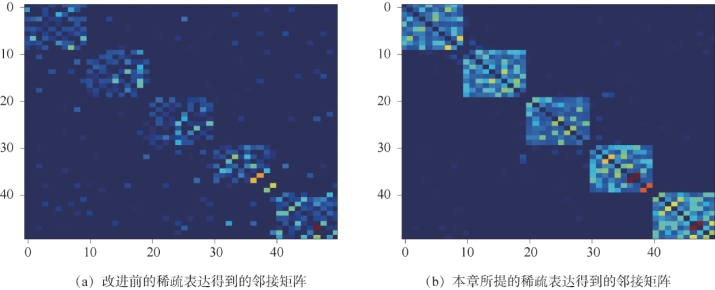
图4-20　基于改进前后的稀疏表达得到的邻接矩阵对比(www.xing528.com)

（2）两种不同模态数据下的图邻接矩阵构造

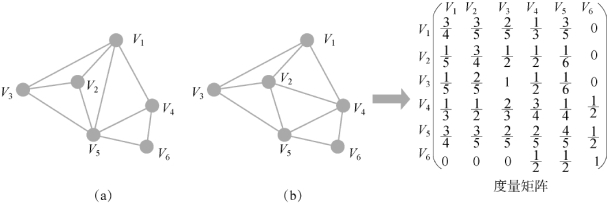
图4-21　两个不同的图以及它们的相似度量矩阵

由图4-21可以看出，当图4-21（a）和（b）中的顶点v6和v1，v2，v3都不存在连接关系时，在度量矩阵中对应的矩阵元素均为0，即它们之间不存在任何关联关系。所以当所有模态的稀疏图邻接矩阵均能体现样本数据之间的类别关系时，上述方法得到的两种不同模态数据间的度量矩阵能很好地反映两者之间的语义关系。

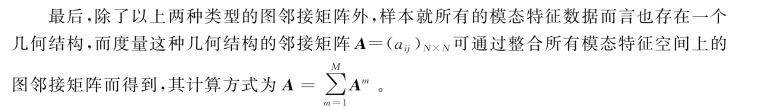
3.图正则约束项

本节将构造的三种不同类型的图邻接矩阵引入到基于非负矩阵分解模型的多模态特征联合表达中，在公式（4-47）中添加图正则约束项，使得MSG-DNMF算法学习到多模态特征数据的共享表达，同时能够原始模态特征数据中不同的几何结构，避免了某些具有较大残差的模态特征数据在联合分解过程中产生偏差，从而进一步提升MSG-DNMF算法的联合表达效果。事实上，在公式（4-47）中使用图正则约束项主要体现在两个方面：一方面，在第一层非负矩阵分解的过程中，希望每个模态的原始数据在经过非负分解后仍能保持样本在原有特征空间中的几何关系；另一方面，在第二层非负矩阵分解的过程中，希望不同模态的样本数据在分解后的共享空间中能够保持一种语义关联关系，同时样本数据也能从整体上保持在所有模态特征空间上的几何结构。

首先，在每个模态特征下对样本与样本之间的相关性采用二分图进行表示。由于公式（4-47）中P m表达的每个模态特征下的基本语义概念，而V m表达的是该模态特征空间下样本的高层语义主题。因此，可以从高层语义主题上建立样本数据之间的关联关系，使得样本能够在每个模态特征的语义主题上保持原始模态特征数据的几何结构。单一模态特征数据下的二分图Ω（V m）表示如下：

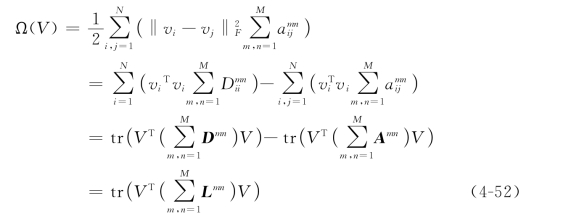
其次，在两个不同模态特征空间下对样本之间相关性采用二分图进行表示。由于公式（4-47）中第二层非负矩阵分解V m=Q m V中，V表示所有模态数据之间的共享子空间，因此，只需要在空间V上建立样本之间的相关性约束。其二分图的表示形式如下：注意的是，当m=n时，有Ω（V）=tr（V T LV），L=D-A，此时Ω（V）的物理意义为当样本在所有模态特征数据上具有关联关系时，它们在共享空间V上也有着相同的邻接关系。因此，公式（4-11）中的图正则约束项既能保证学习到的共享空间V保持样本在任意两个不同模态特征空间上的几何结构，也能保持样本在所有模态特征数据上的几何关系。

最后，将公式（4-47）中的双层非负矩阵分解模型与公式（4-51）、公式（4-52）中的Ω（V m）和Ω（V）进行结合，同时将P m，Q m的正交约束加到目标函数中，便得到MSG-DNMF算法的最终目标函数：

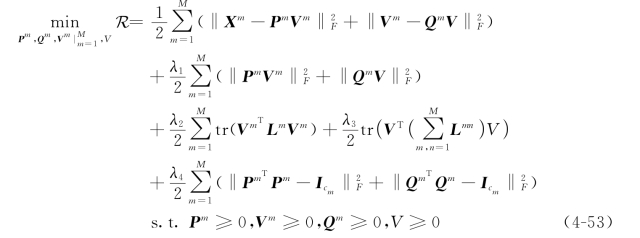
在上述公式中，第一项为双层非负矩阵分解项，用于从多模态特征数据中学习到每个模态特征数据中特有的主题字典系数V m以及它们所共享的语义主题V；第二项中的‖P m V m‖2F和‖Q m V‖2F则是为了防止过拟合；第三项和第四项是用于表征样本在单模态特征空间上几何分布关系以及在不同模态特征上的关联关系；而最后一项为正交约束项使得算法模型能够学习更好的局部特征，此项也可以作为目标函数的约束条件；λ1、λ2、λ3、λ4为不同正则约束项的平衡参数。